题目
题目描述
欢乐岛上有个非常好玩的游戏,叫做“紧急集合”。在岛上分散有N个等待点,有N-1条道路连接着它们,每一条道路都连接某两个等待点,且通过这些道路可以走遍所有的等待点,通过道路从一个点到另一个点要花费一个游戏币。
参加游戏的人三人一组,开始的时候,所有人员均任意分散在各个等待点上(每个点同时允许多个人等待),每个人均带有足够多的游戏币(用于支付使用道路的花费)、地图(标明等待点之间道路连接的情况)以及对话机(用于和同组的成员联系)。当集合号吹响后,每组成员之间迅速联系,了解到自己组所有成员所在的等待点后,迅速在N个等待点中确定一个集结点,组内所有成员将在该集合点集合,集合所用花费最少的组将是游戏的赢家。
小可可和他的朋友邀请你一起参加这个游戏,由你来选择集合点,聪明的你能够完成这个任务,帮助小可可赢得游戏吗?
输入格式
第一行两个正整数N和M(N<=500000,M<=500000),之间用一个空格隔开。分别表示等待点的个数(等待点也从1到N进行编号)和获奖所需要完成集合的次数。 随后有N-1行,每行用两个正整数A和B,之间用一个空格隔开,表示编号为A和编号为B的等待点之间有一条路。 接着还有M行,每行用三个正整数表示某次集合前小可可、小可可的朋友以及你所在等待点的编号。
输出格式
一共有M行,每行两个数P,C,用一个空格隔开。其中第i行表示第i次集合点选择在编号为P的等待点,集合总共的花费是C个游戏币。
输入输出样例
6 4 1 2 2 3 2 4 4 5 5 6 4 5 6 6 3 1 2 4 4 6 6 6
5 2 2 5 4 1 6 0
说明/提示
提示:
40%的数据中N<=2000,M<=2000
100%的数据中,N<=500000,M<=500000
分析
这道题建议自己画图理解:
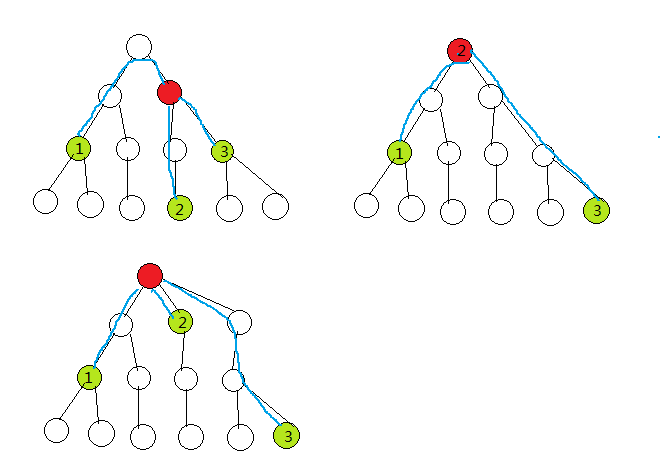
求三个人之间的最短路,原则还是不走重复路
顺着这个思路,那么集合的点必定会在某两个点的路径上
进一步,答案的集合点便是三点中任意两点的路径的交点,
得到结论:三点中任意两点的路径之和为答案路径的两倍(然而感觉没啥用)
再进一步:这个交点是某两点的LCA,(不是LCA路径就有重的啊)
其实到这里就差不多了,直接枚举三个LCA算答案就好(我就是这么干的)
——然而其实大佬是这样的:
NO1. 三个点中,有至少两个LCA是一样的(深度浅的那一个LCA)
NO2.剩下的那一个LCA就是聚集点
代码:

1 /**************************** 2 User:User:Mandy.H.Y 3 Language:c++ 4 Problem:luogu4281 Gather 5 Algorithm: 6 Score 7 ****************************/ 8 #include<bits/stdc++.h> 9 10 using namespace std; 11 12 const int maxn = 5e5 + 5; 13 14 int n,m,size; 15 int dep[maxn],father[maxn],top[maxn],cnt[maxn]; 16 int dis[maxn]; 17 int first[maxn]; 18 19 struct Edge{ 20 int nt,v; 21 }edge[maxn << 1]; 22 23 char *TT,*mo,but[(1 << 15) + 2]; 24 #define getchar() ((TT == mo && (mo = ((TT = but) + fread(but,1,1 << 15,stdin)),TT == mo)) ? -1 : *TT++) 25 template<class T>inline void read(T &x){ 26 x = 0;bool flag = 0;char ch = getchar(); 27 while(!isdigit(ch)) flag |= ch == '-',ch = getchar(); 28 while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar(); 29 if(flag) x = -x; 30 } 31 32 template<class T>void putch(const T x){ 33 if(x > 9) putch(x / 10); 34 putchar(x % 10 | 48); 35 } 36 37 template<class T>void put(const T x){ 38 if(x < 0) putchar('-'),putch(-x); 39 else putch(x); 40 } 41 42 void file(){ 43 freopen("4281.in","r",stdin); 44 // freopen("4281.out","w",stdout); 45 } 46 47 void eadd(int u,int v){ 48 edge[ ++ size].v = v; 49 edge[size].nt = first[u]; 50 first[u] = size; 51 } 52 53 void readdata(){ 54 read(n);read(m); 55 for(int i = 1;i < n; ++ i){ 56 int u,v; 57 read(u);read(v); 58 eadd(u,v);eadd(v,u); 59 } 60 } 61 62 void dfs(int u,int f,int d){ 63 top[u] = u;father[u] = f; 64 dep[u] = d;cnt[u] = 1; 65 int son = 0,mcnt = 0; 66 67 for(int i = first[u];i;i = edge[i].nt){ 68 int v = edge[i].v; 69 if(v == f) continue; 70 dis[v] = dis[u] + 1; 71 dfs(v,u,d + 1); 72 cnt[u] += cnt[v]; 73 if(mcnt < cnt[v]){ 74 mcnt = cnt[v]; 75 son = v; 76 } 77 } 78 if(son) top[son] = u; 79 } 80 81 int find(int x){ 82 return top[x] == x ? x : top[x] = find(top[x]); 83 } 84 85 int LCA(int x,int y){ 86 if(find(x) == find(y)) return dep[x] < dep[y] ? x : y; 87 else return dep[top[x]] < dep[top[y]] ? LCA(x,father[top[y]]) : LCA(y,father[top[x]]); 88 } 89 90 void work(){ 91 92 dfs(1,0,1); 93 94 while(m -- ){ 95 96 int a,b,c; 97 read(a);read(b);read(c); 98 99 int anc1,ans = 0,cur = 0,anc2,ans1; 100 101 anc1 = LCA(a,b); 102 anc2 = LCA(anc1,c); 103 cur = dis[a] + dis[b] - (dis[anc1] << 1); 104 cur += dis[c] + dis[anc1] - (dis[anc2] << 1); 105 ans = cur;ans1 = anc1; 106 107 anc1 = LCA(b,c); 108 anc2 = LCA(anc1,a); 109 cur = dis[b] + dis[c] - (dis[anc1] << 1); 110 cur += dis[a] + dis[anc1] - (dis[anc2] << 1); 111 if(cur < ans) ans = cur,ans1 = anc1; 112 113 anc1 = LCA(a,c); 114 anc2 = LCA(anc1,b); 115 cur = dis[a] + dis[c] - (dis[anc1] << 1); 116 cur += dis[b] + dis[anc1] - (dis[anc2] << 1); 117 if(cur < ans) ans = cur,ans1 = anc1; 118 119 put(ans1); 120 putchar(' '); 121 put(ans); 122 putchar(' '); 123 124 /* 125 126 DALAO的做法: 127 a1 = lca(a,b),b1 = lca(b,c),c1 = lca(c,a); 128 dis = 0; 129 if(a1 == b1) ans = c1; 130 else if(b1 == c1) ans = a1; 131 else if(c1 == a1) ans = b1; 132 133 dis = dep[a] + dep[b] + dep[c] - dep[a1] - dep[b1] - dep[c1]; 134 135 136 */ 137 } 138 } 139 140 int main(){ 141 // file(); 142 readdata(); 143 work(); 144 return 0; 145 }
