Shi J. and Malik J. Normalized cuts and image segmentation. In IEEE Transactions on Pattern Analysis and Machine Intelligence.
概
在Digital Image Preprocessing的书上看到了这个算法, 对于其公式结果的推出不是很理解, 于是下载下来看了看. 本文主要讲的是一种利用图结构进行图像分割的算法.
主要内容
假设(f(x, y), x=1,2,cdots M, y=1,2,cdots N)为一张图片, 我们想要对其进行分割. 给定某一个距离函数, 可以用于衡量任意两点(i, j)的相似度:
[w_{ij} = w(i, j).
]
把图片的每一个pixel看成一个节点, pixel和pixel之间的边为一条无向边, 则整体构成了一个无向的图 (G = (V, E)), 每条边的权重如上所述是(w_{ij}), 故易知(w_{ij} = w_{ji}). 我们的目标是将图分成相斥的两块(A, B), 即满足:
[A �igcup B = V, A �igcap B = empty.
]
以往的做法是, 找到一个分割, 使得下列指标最小:
[cut(A, B) = sum_{i in A, j in B} w_{ij},
]
但是这种策略往往会导致不均匀的分割, 即最角落里的元素被单独分割出来:
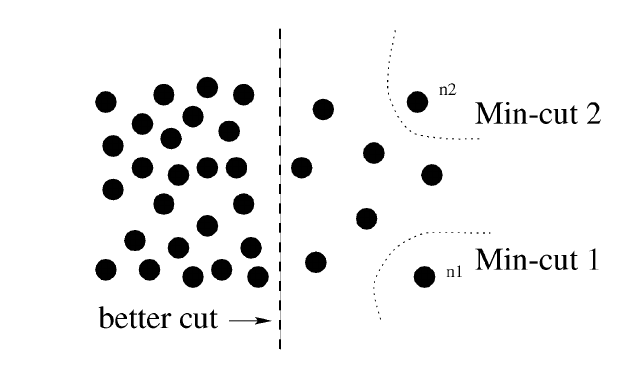
于是作者提出了一种新的指标:
[Ncut(A, B) = frac{cut(A, B)}{assoc(A, V)} + frac{cut(A, B)}{assoc(B, V)},
]
其中(assoc(A, V) = sum_{i in A, j in V} w_{ij}).
注意到:
[Ncut(A, B) = frac{cut(A, B)}{cut(A, B) + assoc(A, A)} + frac{cut(A, B)}{cut(A, B) + assoc(B, B)},
]
所以只有到(assoc(A, A), assoc(B, B))都足够大的时候Ncut才会足够小, 这说明该指标更关注了内部的一种紧密性.
求解
令
[x_i = +1, ext{ if } i in A, quad x_i = -1 ext{ if } i in B \
d_i = sum_{j}w_{ij}.
]
则
[Ncut(A, B) = frac{sum_{x_i > 0, x_j < 0} -w_{ij}x_i x_j}{sum_{x_i > 0}d_i}
+frac{sum_{x_i < 0, x_i > 0} -w_{ij}x_i x_j}{sum_{x_i < 0}d_i}.
]
容易证明(但是不容易想到):
[[frac{1+x}{2}]_i = x_i = +1, : ext{if } i in A, quad
[frac{1+x}{2}]_i = 0, : ext{if } i in B.
]
[[frac{1-x}{2}]_i = -x_i = +1, : ext{if } i in B, quad
[frac{1-x}{2}]_i = 0, : ext{if } i in A.
]
令
[[W]_{ij} = w_ij, \
D_{ii} = d_i,
]
且(D_{ii})为对角矩阵.
所以我们能够证明以下事实:
[4cdot cut(A, B) = (1+x)^T W (1 - x) \
4 cdot assoc(A, V) = 2cdot (1 + x)^T D 1 = (1 + x)^T D (1 + x) \
4 cdot assoc(B, V) = 2cdot (1 - x)^T D 1 = (1 - x)^T D (1 - x) \
assoc(V, V) = sum_i d_i = 1^T D 1 \
(1 + x)^T D (1 - x) = 0.
]
又注意到:
[sum_{x_i > 0, x_j < 0} -w_{ij} x_i x_j = sum_{x_i > 0} [d_i - sum_{x_j >0} w_{ij}] = frac{1}{4}(1 + x)^T (D - W) (1 + x),
]
于是同理可证:
[(1 + x)^TW(1 - x) = (1 + x)^T (D - W)(1 +x) = (1 - x)^T (D - W)(1 -x) .
]
令
[k = frac{assoc(A, V)}{assoc(V, V)},
]
则
[1 - k = frac{assoc(B, V)}{assoc(V, V)}.
]
综上可得:
[ Ncut(A, B) = frac{cut(A, B)}{k1^T D1} + frac{cut(A, B)}{(1-k)1^TD1} = frac{cut(A, B)}{k(1-k)1^TD1}.
]
又
[�egin{array}{ll}
&[(1 + x) - b(1-x)]^T (D-W)[(1+x) - b(1-x)] \
=& (1+x)^T(D-W)(1+x) + b^2 (1-x)^T(D-W) \
&- 2b (1+x)^T(D-W)(1-x) \
=&4(1+b^2)cut(A, B) - 2b (1 + x)^TD(1-x) + 2b(1 + x)^T W(1-x) \
=&4(1+b^2)cut(A, B) - 0 + 8b cut(A, B) \
=&4(1 + b)^2 cut(A, B).
end{array}
]
又
[(1 + frac{k}{1-k})^2 = frac{1}{(1-k)^2},
]
故
[4cdot Ncut(A,B) = frac{4(1+b)^2}{b1^TD1} = frac{[(1 + x) - b(1-x)]^T (D-W)[(1+x) - b(1-x)]}{b1^TD1}, \
b = frac{k}{1-k}.
]
令(y = (1 + x) - b(1 - x)), 且
[y^TDy = sum_{x_i > 0}d_i + b^2 sum_{x_i < 0}d_i = b( sum_{x_i < 0}d_i + b sum_{x_i < 0}d_i) = b1^TD1.
]
[4 cdot Ncut(A, B) = frac{y^T(D-W)y}{y^TDy}.
]
故
[min_x Ncut(A, B) = min_y frac{1}{4} frac{y^T(D-W)y}{y^TDy}, \
mathrm{s.t.} quad y_i in {1, 1 - b}.
]
倘若我们能放松条件至实数域中, 此时只需要通过求解下列系统:
[(D-W)y = lambda Dy Leftrightarrow D^{-frac{1}{2}}(D-W)D^{-frac{1}{2}} z = lambda z, z = D^{frac{1}{2}}y.
]
需要注意的是:
[(D-W)1 = 0,
]
此时(z_0 = D^{frac{1}{2}}1),
故(1)实际上上述系统的一个解, 且对应最小的特征值, 但其不是我们所要的解. 因为(y)必须要还满足:
[y^T D 1 = sum_{x_i > 0}d_i - b sum_{x_i < 0} d_i = 0,
]
这意味着, 我们要的恰恰是
[D^{-frac{1}{2}}(D-W)D^{-frac{1}{2}} z = lambda z, z = D^{frac{1}{2}}y
]
的倒数第二小的特征值对应的特征向量(z_1), 于是(y_1 = D^{-frac{1}{2}}z_1).
相似度
文中采用如下的计算方式:
[w_{ij} =
left {
�egin{array}{ll}
e^{-|F_i - F_j|^2 / sigma^2_I} cdot e^{-|X_i - X_j|^2 / sigma^2_X} & ext{if } |X_i - X_j| < r \
0 & ext{else}.
end{array}
ight.
]
其中(F)对应颜色之类的距离, 如直接取密度值, 而(X)对应空间距离, (r)限定了搜索范围, 同样会导致(W)变成系数矩阵, 对应特征求解加速有帮助.
总的算法流程
- 计算权重矩阵(W)以及(D);
- 通过
[D^{-frac{1}{2}}(D-W)D^{-frac{1}{2}} z = lambda z
]
计算得到倒数第二小的特征值所对应的特征向量(z_1)并令(y_1=z_1);
- 通过某种方法(如网格搜索)找到一个阈值(t):
[x_i = 1, : ext{if }y_i > t, : ext{else } -1.
]
且(x)的划分下[Ncut(A, B)
]
较小.
- 对于(A, B)可以重复上述分割过程, 直到满足区域数目或者其它某种条件(比如文中说的特征向量的分布过于均匀时停止).
skimage.future.graph.cut
skimage.future.graph.cut
