@article{lu2017the,
title={The expressive power of neural networks: a view from the width},
author={Lu, Zhou and Pu, Hongming and Wang, Feicheng and Hu, Zhiqiang and Wang, Liwei},
pages={6232--6240},
year={2017}}
概
Universal approximation theorem-wiki, 这个定理分成俩个部分, 第一个部分是Unbounded Width Case, 这篇文章是Bounded Width Case (ReLu网络).
主要内容
定理1

另外, 定理1中的网络由若干个(视(epsilon)而定) blocks排列而成, 每个block具有以下性质:
- depth: 4n+1, n+4 的神经网络
- 在一个范围外其“函数值”为0
- 它能够存储样本信息
- 它会加总自身的信息和前面的逼近信息
定理2

定理3
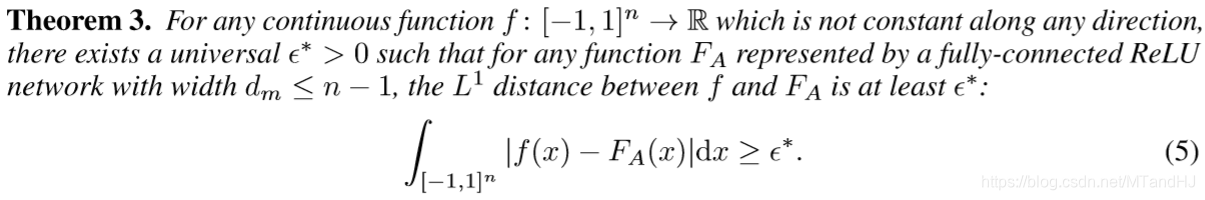
定理4

定理1的证明
因为主要关注定理1, 所以讲下这个部分的证明(实际上是因为其它懒得看了).
假设(x = (x_1, x_2,ldots, x_n))为输入, (f)是(L^1)可积的, 对于任意的(epsilon > 0), 存在(N > 0)满足
定义下列符号:
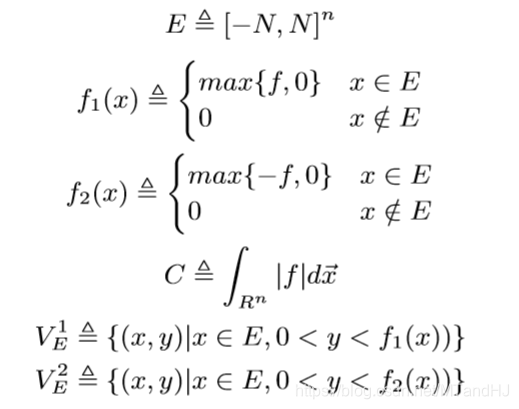
则我们有:
对于(i=1, 2), 既然(V_E^i)是可测的(且测度小于(+infty)), 则我们能找到有限个(n+1)维的矩体去逼近(原文用了cover, 但是我感觉这里用互不相交的矩体才合理), 并有
不出意外(Delta)应该就是.
假设(J_{j,i})有(n_i)个, 且
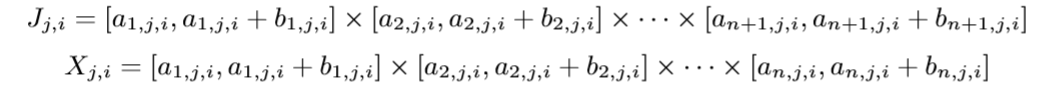
每一个(J_{j, i})对应一个指示函数:
则
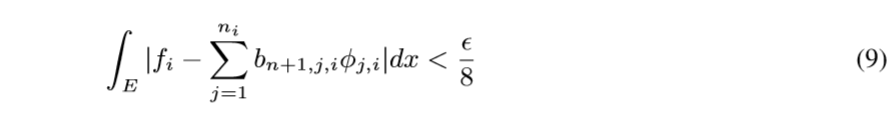
这个在实变函数将多重积分, 提到的下方图形集有讲到.
于是我们有((-f_1-f_2+f_1+f_2-f+f)然后拆开来就可以得到不等式)
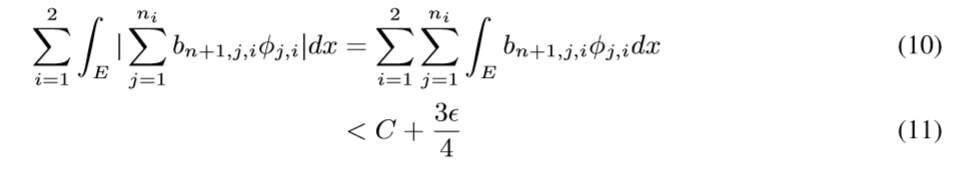
现在我们要做的就是通过神经网络拟合(varphi_{j,i})去逼近(phi_{j,i}), 使得
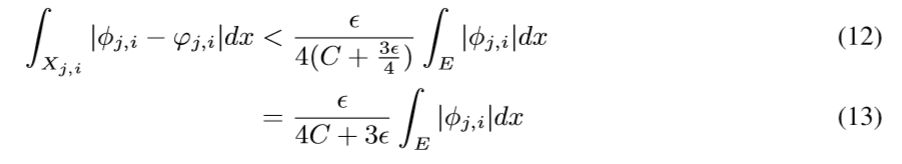
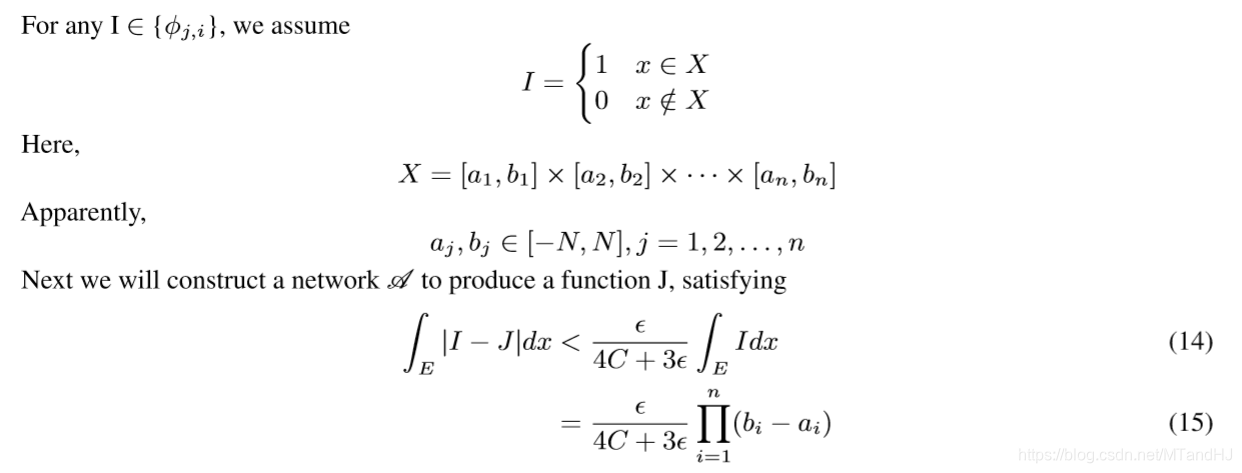
现在来讲, 如果构造这个神经网络:
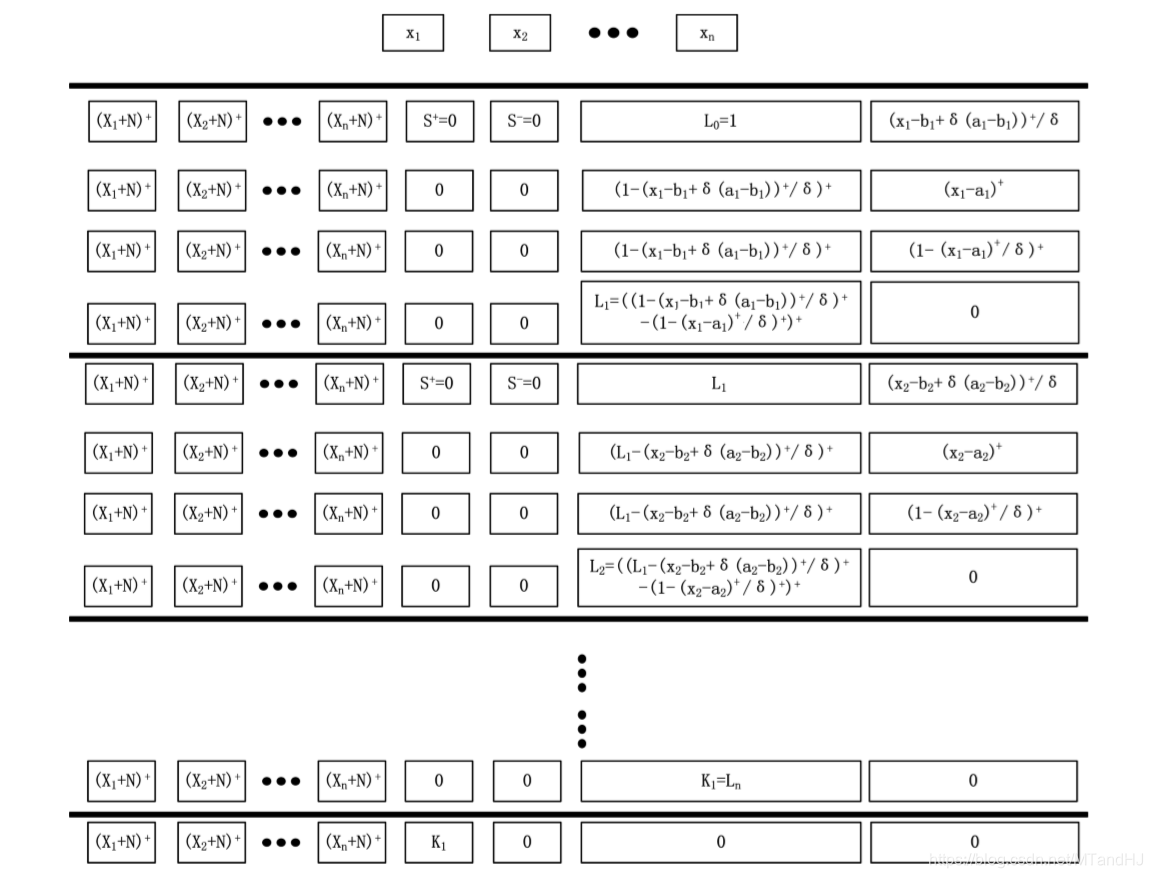
一个block有4n+1层, 每层的width是n+4, 注意到所有层的前n个Node都是一样的用来保存样本信息. 我们用(R_{i, j, mathscr{B_k}}, i=1, 2, 3, 4, j=1,ldots,n+4, k=1,ldots, n,) 表示第(k)个Unit(每个Unit有4层)的第(i)层的第(j)个Node.
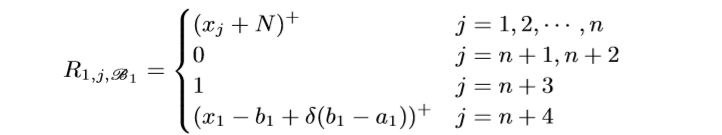
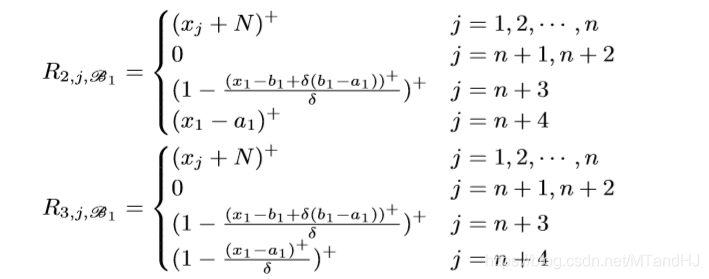

注意: (R_{2, n+3, mathscr{B_1}})应该是((x_1-a_1)^+/delta), 最开始的结构图中的对的. 我们来看一下, 什么样的(x=(x_1, ldots, x_n)), 会使得(L_1)不为0.
如果(x_1=a_1+delta(b_1-a_1)+epsilon), 这里(epsilon>0)是一个任意小量, 和上文中的(epsilon)没有关系. 此时(当(delta<1/2))
当(delta)足够小的时候
此时(L_1=1), 类似地, 可以证明, 当(delta ightarrow 0)的时候, (x_1 in (a_1+delta(b_1-a_1),b_1-delta(b_1-a_1)))时, (L_1=1), 否则为0.
(R_{i, j, mathscr{B_k}})的定义是类似的, 只是
可以证明, 当(delta
ightarrow 0), 且(x_t in (a_t + delta(b_t-a_t),b_t-delta(b_t-a_t)), t=1,2,ldots, k)的时候, (L_k=1.), 这样我们就构造了一个指示函数, 如果这个这函数对应的(i)为1则将(L_n)存入n+1 Node, 否则 n+2 Node (实际上, 我感觉应该存的是(b_{n+1,j,i}L_n)), 则

这里(mu)相当于(L_n). 所以多个blocks串联起来后, 我们就得到了一个函数, 且这个函数是我们想要的.
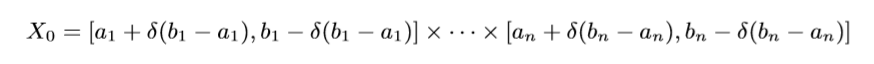
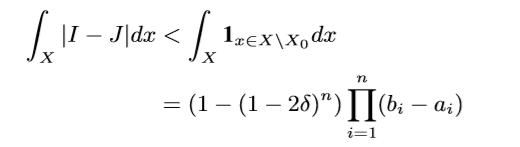
这个直接通过超距体体积计算得来的, 我们只需要取:

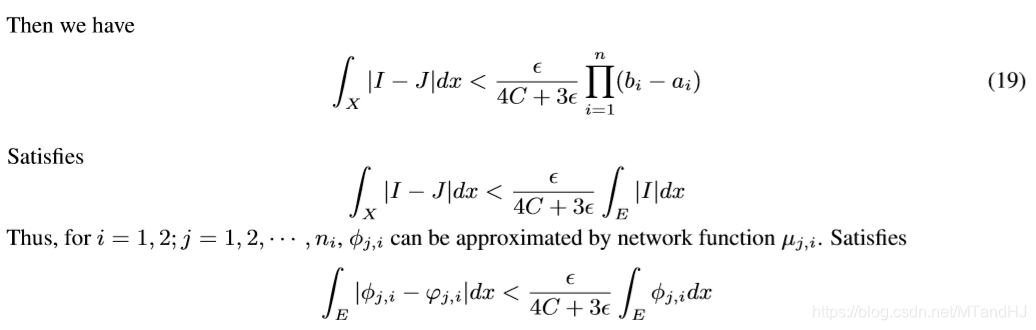
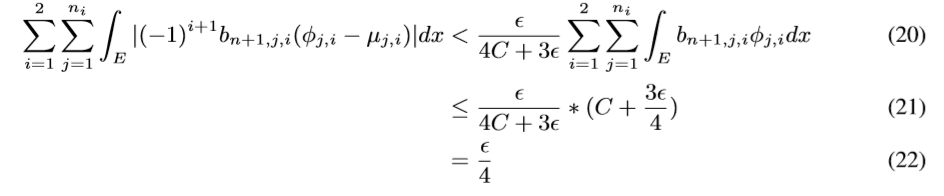
最后
令(g:=sum_{i=1}^2sum_{j=1}^{n_i}(-1)^{i+1}b_{n+1,j,i}mu_{j,i}),便有

此即定理1的证明.