频率学派(古典学派)和贝叶斯学派是数理统计领域的两大流派。
这两大流派对世界的认知有本质的不同:频率学派认为世界是确定的,有一个本体,这个本体的真值是不变的,我们的目标就是要找到这个真值或真值所在的范围;而贝叶斯学派认为世界是不确定的,人们对世界先有一个预判,而后通过观测数据对这个预判做调整,我们的目标是要找到这个世界的概率分布的最优表达。
本科期间学习的概率论与数理统计更多涉及的是频率学派的经典统计学观点,贝叶斯学派的观点也有接触,但是难以分清楚二者的区别。所以整理这篇博客,梳理关于这两个学派的一些知识。
这篇博客从三个方面来整理关于这两个学派的一些重要知识:
1、频率学派和贝叶斯学派的区别
2、先验分布、后验分布和共轭分布
3、最大似然估计和最大后验概率估计
一、频率学派和贝叶斯学派的区别
除了文章开头那段话以外,还可以从以下几个方面来理解两个学派的区别。
1、从三种信息的角度来理解
首先理解三个概念:总体信息、样本信息和先验信息。
数理统计学的任务是通过样本推断总体。把样本视为随机变量时,它有概率分布,称为总体分布。如果我们已经知道了总体的概率分布,那我们得到的这种信息就叫做总体信息。
另一种信息是样本信息,就是从总体中抽取的样本所提供的信息。我们希望通过对样本的加工、整理,从而对总体的分布或对总体的某些数字特征作出统计推断。
总体信息和样本信息放在一起,也称为抽样信息。
第三种信息是先验信息(prior information),就是在抽样之前,根据经验和历史资料,得到的有关统计推断问题中未知参数的信息。
那么基于总体信息和样本信息进行统计推断的理论和方法称为经典(古典)统计学,它的基本观点是:把样本看成是来自于有一定概率分布的总体,所研究的对象是这个总体而不局限于数据本身。
而基于总体信息、样本信息和先验信息进行统计推断的方法和理论则称为贝叶斯统计学,它与经典统计学的主要区别在于是否利用先验信息。在使用样本上也存在差别,贝叶斯统计学重视已出现的样本,对尚未发生的样本值不予考虑。于是贝叶斯学派非常重视先验信息的收集、挖掘和加工,使之形成先验分布而参与到统计推断中,以提高统计推断的效果。
2、从两个学派的争论来理解
频率学派坚持概率的频率解释,对数理统计学中的概念、结果和方法性能的评价等都必须在大量重复的意义上去理解。频率学派对贝叶斯学派的批评主要集中在以下两点:
(1)主观概率以及先验分布的确定。贝叶斯学派提出了主观概率,把主观概念理解为主体对事件发生的概率的相信程度,即不同的人对同一事件的概率可以得到不同的结果。而频率学派认为一个事件的概率要由大量重复试验下的频率来解释,不应该因人而异,必须具有客观性,而且先验分布是主观随意性的产物,不可以接受。
(2)贝叶斯也要以样本分布为出发点,而样本分布通常都是在频率意义上去解释的。可是贝叶斯学派在否定频率学派的同时,却使用了频率学派这个工具。
而贝叶斯学派对频率学派的批评集中在以下两点:
(1)涉及“频率解释”本身。许多应用问题是一次性的,在严格或大致相同条件下让这一个问题重复出现是不可能的。比如预测特朗普当选的概率,预测水灾发生的概率,都是不可能在相同条件下重复出现的,不可能通过重复抽样得到。因此贝叶斯学派认为只能在现有样本的基础上去处理问题。
(2)事前规定精度和可靠度不合理。频率学派基于概率的频率解释,所导出的方法(点估计、区间估计和假设检验)的精度和可靠度是在事前(抽样前)就定下的,称为“事前精度”和“事前可靠度”。贝叶斯学派认为统计推断的精度和可靠度,应该与实际的样本值有关,应当采用“事后精度”和“事后可靠度”。
3、从对未知参数的认识上来理解
频率学派把未知参数θ看成一个未知的固定量,仅把样本看做随机变量,而贝叶斯学派把未知参数也看做是随机变量。
二、先验分布、后验分布和共轭分布
贝叶斯统计学与经典统计学的不同之处在于,贝叶斯统计学在统计推断时除了利用抽样信息外,还利用参数的先验信息,所以贝叶斯方法的一个主要问题是如何确定先验分布。先验分布的确定有很大的主观性和随意性,当先验分布完全未知或部分未知时,如果人为给定的先验分布与实际情形偏离较大时,贝叶斯解的性质就比较差。首先来了解先验分布、后验分布、共轭分布,这是贝叶斯统计学中才有的概念,然后给出基于共轭分布来计算后验分布的方法。
1、先验分布:
参数空间Θ上的任一概率分布都称为先验分布(prior distribution)。用π(θ)来表示随机变量θ的概率函数(当θ为连续型随机变量时,π(θ)表示θ的密度函数;当θ为离散型随机变量时,π(θi)表示概率p(θ=θi),i=1,2,...,n)。
先验分布π(θ)是在抽样样本X之前对参数θ可能取值的认识,在获取样本之后,由于样本X中也包含了θ的信息,故人们对θ的认识发生了变化,于是对θ的取值进行调整,就得到了参数θ的后验分布π(θ|x)。先验分布的两种重要类型是无信息先验分布和共轭先验分布。
2、后验分布:
在获得样本X后,θ的后验分布(posterior distribution)就是在给定X=x条件下θ的条件分布,记为π(θ|x)。求后验分布用的是贝叶斯公式。
(1)连续型
θ为连续型随机变量时,其后验分布的密度函数为:

其中,h(x, θ)=f(x|θ)π(θ)是X和θ的联合密度,f(x|θ)是样本的概率密度函数。而m(x):
![]()
为X的边缘分布。
(2)离散型
当θ是离散型随机变量时,先验分布可用先验分布列{π(θi),i=1,2,...,n}来表示,这时的后验分布是如下离散形式:
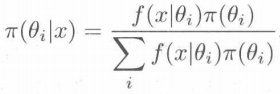
那么后验分布可以看做是人们用总体信息和样本信息(统称为抽样信息)对先验分布作调整的结果,是总体信息、样本信息和先验信息的综合。
3、似然函数和共轭分布
(1)似然函数
对于后验分布计算公式中的f(x|θ),从不同的角度看有不同的含义:
①概率密度函数:若参数θ已知,而x是未知变量,那么描述的是不同样本点的概率,叫做概率密度函数;
②似然函数:若x是已经确定的,而参数θ是变量,那么描述的是对于不同的参数θ,某一个样本出现的概率,一般写作l(θ|x),叫做参数θ的似然函数。
从上面已知,后验分布=样本的密度函数×先验分布/边缘分布,也可以看做:后验分布=似然函数×先验分布/边缘分布。
(2)共轭分布
已知后验分布=似然函数×先验分布/边缘分布,那么如果后验分布与先验分布有相同的形式,比如都服从贝塔分布,那么就称似然函数和先验分布是共轭的,互为共轭分布,先验分布是似然函数的共轭先验分布。对照上面的公式,后验分布为π(θ|x),先验分布为π(θ),似然函数为f(x|θ),π(θ|x) = f(x|θ) × π(θ) / m(x)。计算后验分布的概率密度:

如果计算出来的π(θ|x)和π(θ)有相同的分布类型,那么称f(x|θ)和π(θ)互为共轭分布,π(θ)是f(x|θ)的共轭先验分布。
(3)共轭分布的证明
要证明先验分布为样本概率分布的共轭分布,只要计算后验分布,然后得出后验分布与先验分布形式相同的结论。下面证明泊松分布和伽玛分布是共轭分布。

(4)常见的共轭分布
二项分布与贝塔分布是共轭分布,多线分布和狄里克雷分布是共轭分布,泊淞分布和伽玛分布是共轭分布。
而正态分布的共轭分布是正态分布。
4、后验分布的简化计算
了解了共轭先验分布的概念,那么当先验分布为共轭先验分布(或无信息先验分布)时,可用下面的方法来简化计算后验分布,其他情形只能用上面求解后验分布的公式去求。
(1)后验分布的新表示方法
我们知道,后验密度的计算公式为:

f(x|θ)是样本的密度函数,或者说参数θ的似然函数。m(x)为X的边缘密度,由于m(x)与θ无关,故将1/m(x)看做是一个常数,有
![]()
符号∝表示“正比于”,即符号左边的式子和右边的式子只差了一个与参数θ无关的常数因子。
(2)后验密度的简化计算
于是可以按下面的步骤来简化后验分布的求解过程:
① 写出样本概率密度函数(θ的似然函数)f(x|θ)的核,即f(x|θ)中仅与θ有关的因子;再写出先验密度π(θ)的核,即π(θ)中仅与参数θ有关的因子。
② 写出后验密度的核,即:
![]()
即“后验密度的核”是“样本概率函数的核”和“先验密度的核”的乘积。
③ 在符号∝右边添加一个正则化因子(可以与x有关),就可以得到后验密度:
π(θ|x) = 正则化因子 × {f(x|θ)的核} × {π(θ)的核}
举个例子,设样本服从二项分布,即X~B(n, θ),取参数θ的先验分布为贝塔分布Be(a, b),求θ的后验分布。
解:已知二项分布与贝塔分布是共轭分布,用简化的方法来求后验分布。
样本X的概率分布为:
![]()
那么似然函数(样本密度函数)的核是θx(1-θ)n-x。
贝塔分布概率密度函数的形式为:
![]()
于是参数θ的概率密度函数π(θ)的核为θa-1(1-θ)b-1。
于是得到:
![]()
观察可知,符号最右边的式子为贝塔分布Be(x+a, n-x+b)的核,又已知二项分布与贝塔分布是共轭分布,于是添加正则化因子,构造贝塔分布的密度函数,得到后验密度:
![]()
三、最大似然估计(MLE)和最大后验概率估计(MAP)
统计要解决的问题是,手头有一堆数据,要利用这堆数据去推测模型和参数,而最大似然估计和最大后验概率估计就是推断模型和参数的两种不同方法。
1、最大似然估计
最大似然估计是求参数θ, 使似然函数p(X|θ)最大。频率学派采用最大似然估计来推断模型的参数。最大似然估计的含义是根据已经采集到的样本,希望通过调整模型参数使得这些样本被选中的概率最大。
样本的似然函数为p(X|θ),可以理解为已知样本集合X的情况下,所有样本点同时出现的概率,是关于参数θ的函数,因此最大似然估计就是要最大化似然函数。
最大似然估计的目标函数为:
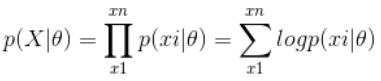
2、最大后验概率估计
最大后验概率估计则是想求参数θ,使p(x|θ)p(θ)即后验概率最大。求得的θ不单让似然函数大,θ本身出现的先验概率也得大。贝叶斯学派采用最大后验概率估计来推断模型的参数。最大后验概率估计的含义是基于对参数的一个先验假设,并根据已经收集到的样本,通过调整参数使得这些样本被选中的后验概率最大。模型参数本身满足某种分布,不再一味地依赖数据样例。
如果以密度函数来进行计算,最大后验概率估计的目标函数就是:

3、二者的联系
最大似然估计比较依赖较大的数据量和大数定律,在样本量较少时,参数估计的结果容易出现较大偏差。
最大后验概率估计允许我们把先验知识加入到估计模型中,这在样本很少的时候是很有用的。但是随着样本量的增大,参数估计的结果主要受数据量的影响,先验假设的影响会越来越小。
如果参数θ服从于均匀分布U(0,1)时,有先验概率为p(θ)=1,此时最大似然估计和最大后验概率估计是等价的。
参考资料:
1、韦来生:《贝叶斯统计》
2、周志华:《机器学习》
3、频率学派还是贝叶斯学派?
https://blog.csdn.net/yH0VLDe8VG8ep9VGe/article/details/78999639
4、详解最大似然估计(MLE)、最大后验概率估计(MAP),以及贝叶斯公式的理解
https://blog.csdn.net/u011508640/article/details/72815981
5、极大似然估计,最大后验概率估计(MAP),贝叶斯估计
https://blog.csdn.net/vividonly/article/details/50722042