最短路径

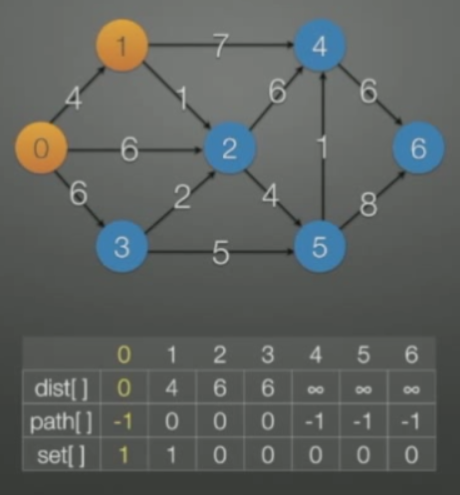
初始化 只有set[0]为1 也就是只有0并入了set中

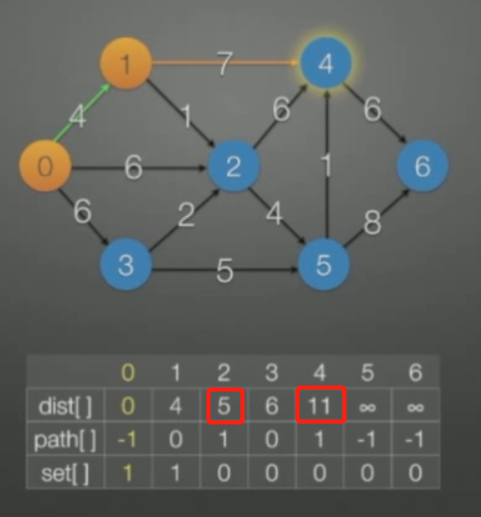
然后从dist中找到了一条最小的4，其节点为1，将1并入set，并入1以后，更新dist

 

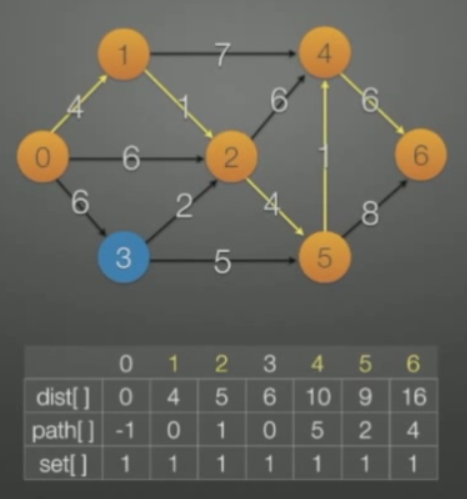
按这个原理循环，将所有的点都并入set中，最终得到顶点0到其它顶点的最短路径dist[ ]，若要得到0到某个顶点i的最短路径，只需找path[i]，例如要求0到6的最短路径，首先找到paht[6]，path[6]=4，然后找path[4]，path[4]=5，又找path[5]，path[5]=2，又找path[2]，path[2]=1，又找path[1]，path[1]=0，再找paht[0]，path[0]=-1，停止，寻找完毕，则从0到6的最短路径为0→1→2→5→4→6

void Dijkstra(int n, int **map)
{
    //map是邻接矩阵 若两个顶点之间无路径 则为999 无穷大
    int i, j;
    int INF = 999;//无穷大
    int *set, *dist, *path;
    dist = new int[n]; //用来存每一趟边的权值，每一趟会更新
    set = new int[n];  //用来存每个顶点是否已并入集合
    path = new int[n]; //用来存路径
    int min, v, v0 = 0;
    for (i = 0; i < n; i++)
    {
        dist[i] = map[0][i];
        set[i] = 0; //开始时每个顶点都未访问
        if (map[v0][i] < INF)
            path[i] = v0;
        else
            path[i] = -1;    
    }
    set[v0] = 1;//v0并入集合
    path[v0] = -1; //v0是起始点故它的path为-1
    for (i = 0; i < n - 1; i++)
    {
        min = INF;
        for(j=0;j<n;j++)
            if (set[j] == 0 && dist[j] < min)
            {
                v = j;
                min = dist[j];
            }
        set[v] = 1; //找到一条最短的边，将其节点并入
        //并入一个新的点以后，要更新dist数组和path数组
        for (j = 0; j < n; j++)
        {
            if (set[j] == 0 && min + map[v][j] < dist[j])
            {
                dist[j] = min + map[v][j];
                path[j] = v; 
              /*这里虽然更新了path 但它不一定是最终的path 
                因为它还没并入set中 以后可能会随着新的顶点的并入 
                path又会改变*/
            }
        }
    }
}