用于计算一类朴素卷积问题。
笔者学习的是这份博客
内容中可能有很多相同之处,敬请谅解。
现在要计算两个一元(n)次多项式(F(x))与(G(x))的乘积,如何计算?
前置知识:多项式的表示方法
一. 系数表示法
对于一个(n)次多项式(F(x)),它可以被表示成
更加形式化的来说,它可以表示成
举个例子,2次多项式,其中(a_0=1,a_1=2,a_2=1)
那么(F(x)=1x^2+2x+1.)这样即可通俗的表示出一个(n)次多项式。
二. 点值表示法
众所周知,两个点确定一个一次函数,三个点确定一个二次函数。
所以,(n+1)个点确定一个一元(n)次多项式。
所以我们可以通过(n+1)个点来表示它。
那么相乘之后的点值如何计算?
比如说两个2次多项式(F(x)=x^2+2x+1)(红色)与(G(x)=3x^2-4x-2)(蓝色),它们的图像如图所示:
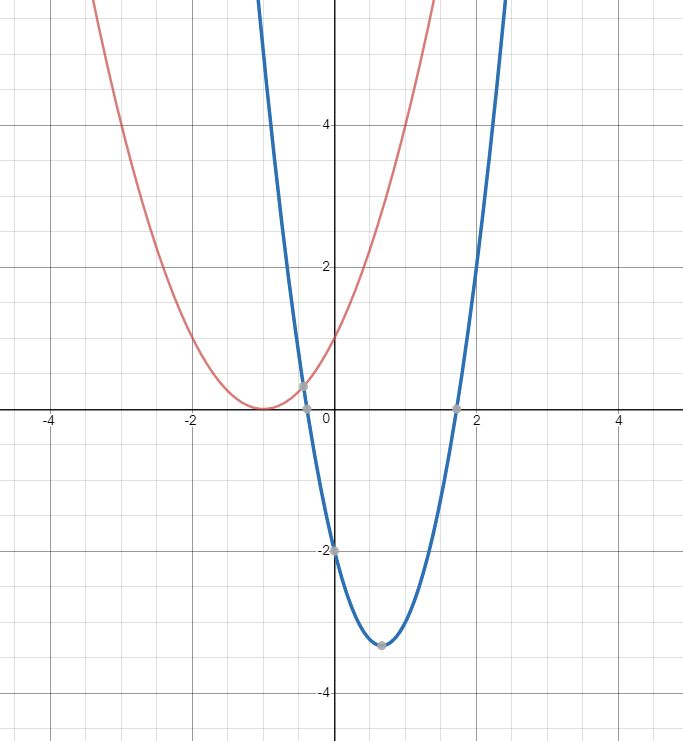
那么观察图中(x=1)时的情况。此时(F(1)=4,G(1)=-3.)
所以,显然,(F(1) imes G(1)=-12).也就是说在(Z=F*G)这一多项式内,带入(1),得到的结果是(-12).
等等,好像有哪里不对。如果说(Z=F*G)的话,那么Z的次数应该是(2n).
那(Z)需要(2n+1)个点来确定。但是原来只需要(n+1)个点,咋办?
很简单,在原来的多项式里每个都多加(n)个点即可。反正多项式已知。
这样就可以用点值来进行操作。也就是说先转成点值,再一乘,再转回来,就是计算流程。
但是好像还是很慢。那么如何优化呢?
复数部分
复数,即形如(a+bi)的数,其中(i^2=-1.) (a)称为实部,(bi)称为虚部。
或者说:在一个数轴上(只有x轴),我们可以表示出任何实数。
那么,多加一维(y轴),也就是类似于平面直角坐标系一样,我们就可以表示出任意一个复数。
所以我们把这个坐标系叫做复平面,其中x轴称为实轴,y轴称为虚轴。
复数运算
复数相加:实部相加,虚部相加,例如
复数相减:同理。
复数相乘:像一次多项式一样相乘。 注意(i^2=-1).
复数相除:
相信大家都学过共轭根式。同样的,复数也有共轭。
即:(a+bi)的共轭为(a-bi)。
这两个复数卡乘在一起一定是个实数。即
所以再除的时候,将分子分母同乘分母的共轭,就可以将分母有理化。
即
复数逆元:
同样的,复数运算在复平面内也有一定规律可循。
考虑在复平面内的两个复数:(借张图)
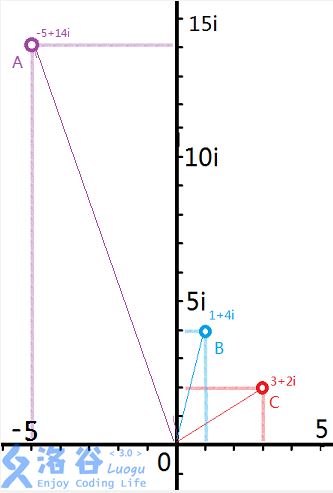
表示的是复数((1+4i))与复数((3+2i))相乘所得的结果:((-5+14i))。
设其中((5,0))点为位置(P),则(angle{POC}=angle{BOA}.)
还有:(overline{OB} imesoverline{OC}=overline{OA}.)
第二个证明:勾股定理。先把(i)消掉。
(overline{OB}^2=a^2+b^2.) (overline{OC}^2=c^2+d^2.)
(overline{OB}^2 imes overline{OC}^2=(a^2+b^2)(c^2+d^2)=a^2c^2+a^2d^2+b^2c^2+b^2d^2.)
(overline{OA}^2=(ac-bd)^2+(ad+bc)^2=a^2c^2+a^2d^2+b^2c^2+b^2d^2.)得证。
我们将复数中,复数向量的长度称为模长,向量与x轴正方向的夹角称为幅角。
根据上面的东西:复数相乘时,模长相乘,幅角相加。
单位根
一个n次的单位根即为方程(x^n=1)的复数解。
考虑这样一个图:
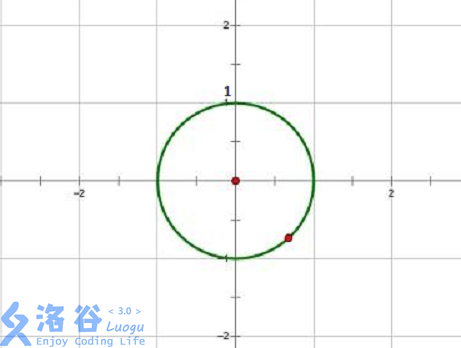
其中圆上的所有复数模长都是1,这个圆称为单位圆。
考虑(|x|)的取值范围:
如果(|x|<1),那么(|x^n|<1)(模长*模长,越乘越短)
如果(|x|>1),那么(|x^n|>1)(模长*模长,越乘越长)
所以一定有(|x|=1),即点一定在这个单位圆上。
那么还有一条,就是一个n次的单位根共有n个,并且从(1,0)开始,每次逆时针走(frac{1}{n})个圆周。分别称为(omega_{n}^{0},omega_{n}^{1},...omega_{n}^{n-1}.)(逆时针编号!!!)
其实还有(kgeq n)和(k<0)的单位根,本质上就模个n就可以了,这里不再多加考虑。
有关单位根也有很多性质:
- (omega_{n}^{0}=1)
- (omega_{n}^{k}=(omega_{n}^{1})^k),很好理解,就是每次转(frac{1}{n})圆周。
- (omega_{n}^{j} imes omega_{n}^{k}=omega_{n}^{j+k}.)
证明:很简单,代入性质2即可。
根据3,有:
再设两个n/2项多项式:
那么有(F(x)=FL(x^2)+x*FR(x^2).)(不懂可以自己设一下代入进去)
下面,我们来代入单位根,看看会有什么神奇的事情发生。
比如说我们代一个(omega_{n}^{k}(k<frac{n}{2}):)
其中,((omega_{n}^{k})^2=omega_{n}^{2k}=omega_{frac{n}{2}}^{k}.)然后代入:
然后呢?有啥用?
不难发现,如果我们知道了(FL(x),FR(x))在x取(omega_{frac{n}{2}}^{0},omega_{frac{n}{2}}^{1}...omega_{frac{n}{2}}^{frac{n}{2}-1})下的所有值,我们就可以知道(F(x))在x取(omega_{n}^{0},omega_{n}^{1}...omega_{n}^{frac{n}{2}-1})下的所有值(代回原式)。
但是这还不是全部啊,剩下那个部分怎么办?
没关系,考虑(k<frac{n}{2}),代入(omega_{n}^{k+frac{n}{2}})时的情况。
其中,((omega_{n}^{k+frac{n}{2}})^2=omega_{n}^{2k+n}.)
故
(模性质)
(性质3 延展)
(取反性质)
然后观察这个式子和前面式子的区别,发现就是把+号改成了-号。也就是说我们可以通过那组数据来算出当(k>frac{n}{2})时的情况。这就是加速DFT的原理。
IDFT
至此,我们已经可以将其转化为点值,那么如何还原回来呢?使用IDFT插值。
考虑一个向量(c_0,c_1...c_{n-1}),满足$$c_k=sum _{i=0}{n-1}(omega_{n}{-k})^i imes y_i.$$
其中(y_i)表示乘出来的点的y坐标。
那么,这个式子也就代表一个以(y)为系数的方程在取(x=omega_{n}^{-k})时的复数解。
我们尝试着来化简一波。
发现后面标红的东西就是一个等比数列,那么我们可以直接计算。即
我们设这个东西为公式(Z.)
于是就有
观察函数(Z)的相关性质。
赫然发现:我们带进去的是单位根!单位根啥性质来着?(X^n=1!)
也就是说当(X≠1),也就是(k≠0)时,原式(=0.) (分子为0)
那么(X=1)时,也就是(k=0)时呢?这时候这个求和公式就不管用了,带回原式算,发现由于(1^i=1)(i是自然数),那么(Z(x)=n.)
所以说,什么情况下带进去的值(k=0)呢?显然是(j-k)的时候!此时单项(=na_k).
否则的话会乘一个0,答案固然也是0.
所以有:$$c_k=na_k$$(飞跃性的一步!!!)
回顾整个式子,发现我们算(c)的时候连(a)的影子都没有,现在我们竟然推出了一个和(a)有关的关系式!太神奇了!这就是(IDFT)的原理。
至此,( ext{FFT})的重要部分已经全部介绍完毕,下面进入代码实现与细节处理部分。
代码实现
朴素DFT:
complex < double > omega(const int n , const int k) { // 单位根
complex < double > ret = {cos(2 * Pi / n * k) , sin(2 * Pi / n * k)};
if(!inv) return ret;
else return conj(ret);
}
void DFT(complex < double > a , const int n) {
if(n == 1) return ;
static complex < double > buf[MAXN];
const int m = n / 2;
for(int i = 0; i < m; i++) {
buf[i] = a[(i << 1)];
buf[i + m] = a[(i << 1 | 1)];
}
copy(buf , buf + n , a);
complex < double > *a1 = a , *a2 = a + m;
DFT(a1 , m); DFT(a2 , m);
for(int i = 0; i < m; i++) {
complex < double > w = omega(n , i);
buf[i] = a1[i] + w * a2[i];
buf[i + m] = a1[i] - w * a2[i];
}
copy(buf , buf + n , a);
}
发现这样的效率显然不行,那么考虑迭代形式。
首先观察分治到最后的二进制位表示:
000 001 010 011 100 101 110 111
0 1 2 3 4 5 6 7
0 2 4 6 - 1 3 5 7
0 4 - 2 6 - 1 5 - 3 7
0 - 4 - 2 - 6 - 1 - 5 - 3 - 7
000 100 010 110 001 101 011 111
然后...我们惊奇的发现最后的二进制位就是之前的二进制位倒过来!TQL!
接着考虑空间优化。
不难发现,由于DFT的两个式子十分相近,所以我们可以只算一次,同时通过技巧性的操作直接覆盖原数组,而不再新开一个。这个操作被称为蝴蝶操作。
蝴蝶操作的代码:
for(int l = 2; l <= n; l <<= 1) {
int m = l / 2;
for(complex < double > *p = a; p != a + n; p += l) {
for(int i = 0; i < m; i++) {
complex < double > t = omega[n / l * i] * p[m + i];
p[m + i] = p[i] - t;
p[i] += t;
}
}
}
然后穿起来,与以前的FFT模板结合即可。
#include <bits/stdc++.h>
#define dbg(x) cerr << #x " = " << x << "
"
#define INF 0x3f3f3f3f
/* do not give up ! */
/* try your best! */
/* Read the meaning clearly! */
typedef long long LL;
typedef long double ld;
typedef unsigned long long ULL;
using namespace std;
template < typename T > inline void inp(T& t) {
char c = getchar(); T x = 1; t = 0; while(!isdigit(c)) {if(c == '-') x = -1; c = getchar();}
while(isdigit(c)) t = t * 10 + c - '0' , c = getchar();t *= x;
}
template < typename T , typename... Args > inline void inp(T& t , Args&... args) {inp(t); inp(args...);}
template < typename T > inline void outp(T t) {
if(t < 0) putchar('-') , t = -t; T y = 10 , len = 1;
while(y <= t) y *= 10 , len++; while(len--) y /= 10 , putchar(t / y + 48) , t %= y;
}
template < typename T > inline T mul(T x , T y , T MOD) {x=x%MOD,y=y%MOD;return ((x*y-(T)(((ld)x*y+0.5)/MOD)*MOD)%MOD+MOD)%MOD;}
const int MAXN = 2097152 + 10;
const double Pi = acos(-1.0);
int ans[MAXN];
struct FastFourierTransform {
complex < double > omega[MAXN] , omegaInverse[MAXN];
void init(const int n) {
for(int i = 0; i < n; i++) {
omega[i] = complex < double > (cos(2 * Pi / n * i) , sin(2 * Pi / n * i));
omegaInverse[i] = conj(omega[i]);
}
}
void Transform(complex < double > *a , const int n , const complex < double > *omega) {
int k = 0;
while((1 << k) < n) ++k;
for(int i = 0; i < n; i++) {
int t = 0;
for(int j = 0; j < k; j++) if(i & (1 << j)) t |= (1 << (k - j - 1));
if(i < t) swap(a[i] , a[t]);
}
for(int l = 2; l <= n; l <<= 1) {
int m = l / 2;
for(complex < double > *p = a; p != a + n; p += l) {
for(int i = 0; i < m; i++) {
complex < double > t = omega[n / l * i] * p[m + i];
p[m + i] = p[i] - t;
p[i] += t;
}
}
}
}
void DFT(complex < double > *a , const int n) {
Transform(a , n , omega);
}
void IDFT(complex < double > *a , const int n) {
Transform(a , n , omegaInverse);
for(int i = 0; i < n; i++) a[i] /= n;
}
}FFT;
int main() {
int nn , mm , x; inp(nn , mm);
nn++ , mm++;
int n = 1; while(n < nn + mm) n <<= 1;
complex < double > a[MAXN] , b[MAXN];
for(int i = 0; i < nn; i++) {
inp(x); a[i].real(x);
}
for(int i = 0; i < mm; i++) {
inp(x); b[i].real(x);
}
FFT.init(n);
FFT.DFT(a , n);
FFT.DFT(b , n);
for(int i = 0; i < n; i++) a[i] *= b[i];
FFT.IDFT(a , n);
for(int i = 0; i < nn + mm - 1; i++) {
ans[i] = static_cast < int > (floor(a[i].real() + 0.5));
cout << ans[i] << " ";
}
return 0;
}
至此,该代码已经可以效率很高地通过P3803一题!完结撒花!
FFT例题将会另外放在一个帖子~