20172323 2018-2019-1 《程序设计与数据结构》第八周学习总结
教材学习内容总结
本周学习了第12章优先队列与堆
- 12.1 堆
- 堆是具有两个附加属性的一棵二叉树,它是一棵完全树,对于每一结点,它小于或等于其左孩子和右孩子,这样定义下的堆是最小堆,如果对于每一结点,它大于或等于其左孩子和右孩子,那么它就是最大堆。
- 最小堆将其最小元素存储在该二叉树的根处,且其根的两个孩子同样也是最小堆。
操作 说明 addElement 将给定元素添加到该堆中 removeMin 删除堆的最小元素 findMin 返回一个指向堆中最小元素的引用
-
如图是一个最小堆
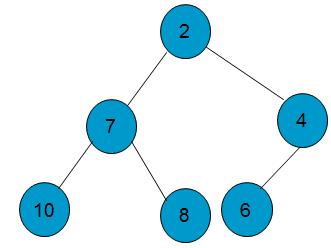
-
addElement方法将给定的Comparable元素添加到堆中的恰当位置处,且维持该堆的完全性属性和有序性属性
如果一棵二叉树是平衡的,及所有叶子都位于h或者h-1层,其中h为log2n,n是树中的元素数目,以及所有h层中的叶子都位于该树的左边,那么该树就被认为是完全的。因为堆是一棵完全树,所以对于新插入的结点只存在一个正确的位置,要么是h层左边的下一个空位置,要么就是h+1层左边的第一个位置(如果h层是满的话)
- 新结点添加之后,将考虑堆的排序性。,该结点将于它的双亲结点进行比较,如果新结点小则要与双亲结点进行互换,之后再沿树往上进行比较直至新值大于双亲或者位于根结点。
- 在堆实现中,我们会对树中的最末一个结点(最末一片叶子)进行跟踪记录。

2添加到堆之后,将于其双亲进行比较上浮直至堆满足其顺序属性 - removeMin操作将删除最小堆中的最小元素并返回他,最小堆中的元素即是它的根结点,为了保持树的合法性,需要有一个能替换根的合法元素,且它是树中最末一片叶子上的元素。将最末一片叶子移至根处之后,又需要将该堆进行重新排序。排序方法需要将该结点与最小孩子进行比较然后逐渐下沉到合适的位置。借用上图,如果将根结点1删去,那么最末叶子6就将成为新的根结点,它将与2、5进行比较最终落在5现在的位置,而2将成为新的根结点。
- 12.2 使用堆:优先级队列
- 优先级队列就是遵循两个排序规则的集合。一是具有更高优先级的项目在先,二是具有相同优先级的项目使用先进先出方法确定其排序。
- 虽然最小堆根本就不是一个队列,但是他却提供了一个高效的优先级队列实现
- 12.3 用链表实现堆
- 堆中结点必须存储指向其双亲的指针。
- 链表实现addElement操作的时间复杂度为O(logn)
- removeMin操作的时间复杂度同样为O(logn)。
- findMin操作时间复杂度为O(1)
- 12.4 用数组实现堆
- 堆的数组实现比链表实现更为简洁。
- 在二叉树的数组实现中,树的根位于位置0处,对于每一结点n,n的左孩子将位于数组的2n+1
处,n的右孩子将位于数组的2(n+1)位置处 - 数组实现不需要确定新结点双亲,时间复杂度与链表实现相同,但数组实现效率更高
- 链表实现与数组实现的removeMin操作的复杂度同为O(logn)
- 12.5 使用堆:堆排序
- 堆排序的由两步构成:添加列表的每个元素,然后一次删除一个元素
- 堆排序的复杂度为O(nlogn)
教材学习中的问题和解决过程
-
问题1:链表实现堆的过程中的addElement操作第一步要确定要插入结点的双亲,为什么在最坏的情况下要从堆的右下结点遍历到根结点之后还要再从根结点遍历到堆的左下结点?
-
问题1解决方案:这个问题我思考了小半个小时,添加的第一步需要确定插入结点的双亲,因为需要比较双亲结点的值与新结点的值,决定新结点是否要上浮。所以最坏的情况应该是新结点一直上浮到根结点,此时按最小堆的定义来看,添加元素这一操作应该是停止了,因为堆顶是最小元素了,它的左孩子和右孩子的值都应该比它要小,所以不需要继续遍历它的左孩子直到左下结点了吧。和同学讨论之后,才发现我的理解错在哪里了。它这里指的是遍历的最坏情况需要从右下结点一直到根再到左下结点,而不是结点互相之间的比较需要让结点上浮之后再次下沉(事实上跟我分析的一样,他也无法做到)。它这里指的是查找确定新结点的双亲结点的最坏情况
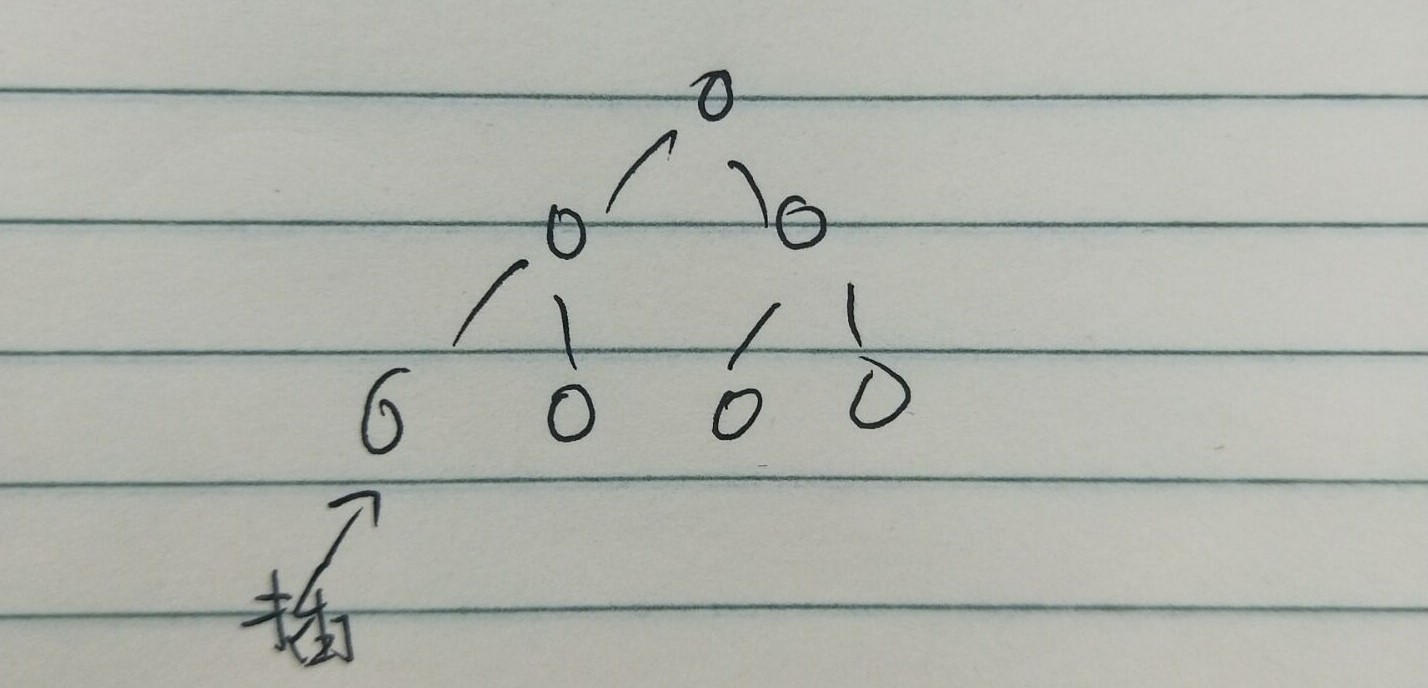
如上丑图,添加元素时刚好遇见满树的情况,需要从右下最后一片叶子开始找起,一直到左下结点,才最终确定要插入的元素的双亲结点。
- 问题2:对书上代码
getNextParentAdd方法的理解 - 问题2解决方案:
HeapNode<T> result = lastNode;
while ((result != root) && (result.getParent().getLeft() != result))
result = result.getParent();
if (result != root)
if (result.getParent().getRight() == null)
result = result.getParent();
else {
result = (HeapNode<T>) result.getParent().getRight();
while (result.getLeft() != null)
result = (HeapNode<T>) result.getLeft();
}
else
while (result.getLeft() != null)
result = (HeapNode<T>) result.getLeft();
return result;
首先教材讲到,这是一个返回指向插入结点的双亲结点的引用。所以就容易理解到,这个方法就是确定新插入结点的双亲结点。也就通过此来决定新添加元素的位置。
一开始,新设一个变量result指向lastNode,即指向最后一片叶子的引用。
接下来通过判断最后一片叶子的情况来确定插入结点的双亲结点,当最后一片叶子不是根结点且同时不是左孩子的时候,就将result的父结点付给result,直到不满足两个条件之一跳出循环。当最后一片叶子是根结点时,已经确定了新结点的双亲结点,可以进入下一步,而如果最后一片叶子是右结点,就说明当前父结点是满的,不能再在当前父结点下添加新元素,所以将result指向result的父亲,方便寻找一个没有满的父结点。下一步,此时result跳出while循环,要么它是根结点,要么它是左孩子。如果它是左孩子,即进入if语句内,判断它的兄弟结点是否为null,如果返回true,那么新添加元素的双亲结点就确定了是result的父结点,而新结点将作为result的右孩子添加到堆中,如果返回false,result将指向这个右孩子,并找到它的最左下的位置添加。如果result是指向根结点的,那么也一直循环到它的最左下位置,添加新元素。
这个问题的解决参考了于欣月同学的博客,她在解释时运用了图文结合的形式,对我理解该问题起了很大帮助
代码调试中的问题和解决过程
-
问题1:测试LinkedHeap类,实现层序输出、前序中序后序各种输出,很不巧的是它出现了乱码的情况
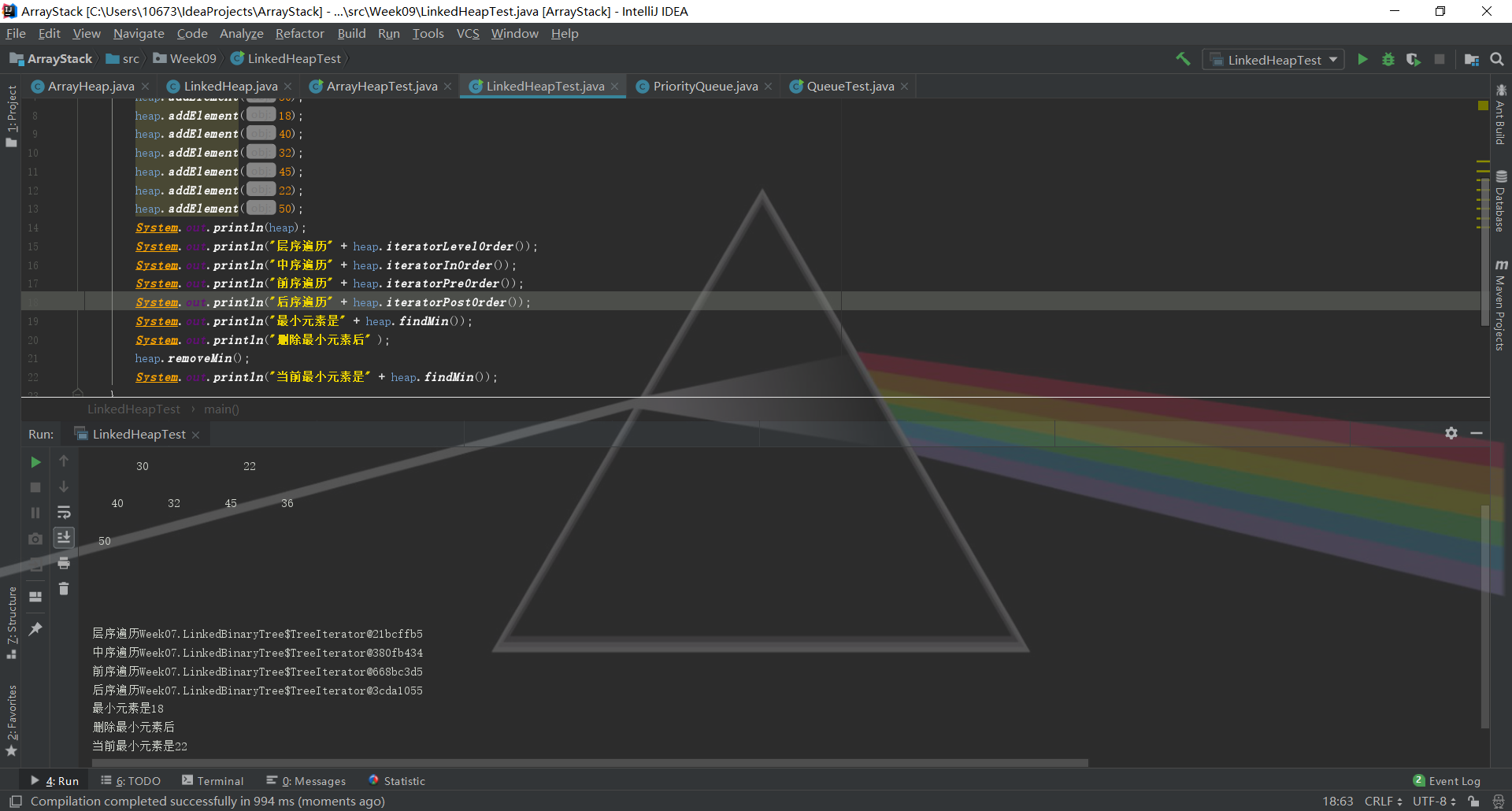
-
问题1解决方案:这个问题的出现充分说明我还没能掌握迭代器的精髓,首先方法的使用就是完全错误的,我还把它当作简单的toString方法在加以使用。所以自然输出不来需要的结果,标准的应该是如图,先设置一个迭代器的对象,通过for循环一个一个调用迭代器里的内容,如图
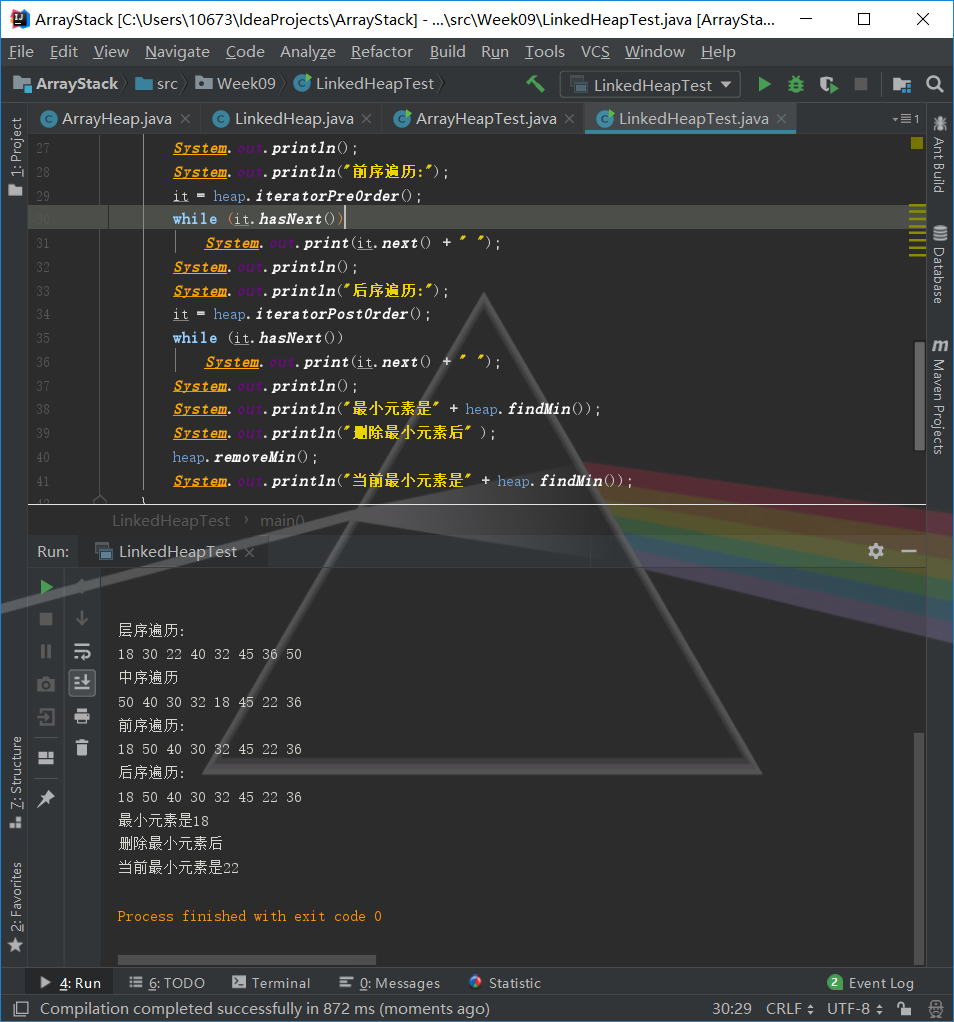
代码托管
上周考试错题总结
- In removing an element from a binary search tree, another node must be ___________ to replace the node being removed.
A .duplicated
B .demoted
C .promoted
D .None of the above - 解析:从二叉查找树中删除一个元素时,必须推选出另一个结点来代替要被删除的那个结点
。demoted意思是降级的,promoted是升级的,从概念来看,替代元素应该是该结点的中序后继者,所以该是c。
- The Java Collections API provides two implementations of balanced binary search trees, TreeSet and TreeMap, both of which use a ___________tree implementation.
A .AVL
B .red/black
C .binary search
D .None of the above - 这好像是13章的内容乱入了吧,TreeSet和TreeMap类使用的是红黑平衡二叉查找树
- The best comparison sort in terms of order is:
A .O(1)
B .O(n)
C .O(log(n))
D .O(nlog(n))
- Linear search has logarithmic complexity, making it very efficient for a large search pool.
A .true
B .false - 线性查找具有线性时间复杂度O(n)。
- Bubble, Selection and Insertion sort all have time complexity of O(n).
A .true
B .false
排序方法 时间复杂度 选择排序 O(n^2) 插入排序 O(n^2) 冒泡排序 O(n^2)
- Insertion sort is an algorithm that sorts a list of values by repetitively putting a particular value into its final, sorted, position.
A .true
B .false - 插入排序通过反复地将某一特定值插入到该列表的某个已排序的子集中来完成对列表值的排序。每一个值只需要插入一次,而不是重复地插入。
结对及互评
- 博客中值得学习的或问题:
- 在我的鞭策与督促之下,某同学的博客又恢复到了以往的超高水平。(他在教材问题中提到了一个
实现优先级队列的二叉堆、d堆、左式堆、斜堆、二项堆都是什么意思?
我翻了一下书,好像没有找到哪里提到了这些概念,所以如果是查找的资料里提到的,希望也能贴出链接来,让我学习学习,不至于落下太多
-
方艺雯的博客写的很棒,提出了很多我没考虑过的问题。
-
基于评分标准,我给谭鑫的博客打分:6分。得分情况如下:
正确使用Markdown语法(加1分)
模板中的要素齐全(加1分)
教材学习中的问题和解决过程, 一个问题加1分
代码调试中的问题和解决过程, 三个问题加3分 -
基于评分标准,我给方艺雯的博客打分:8分。得分情况如下
正确使用Markdown语法(加1分):
模板中的要素齐全(加1分)
教材学习中的问题和解决过程, 两个问题加2分
代码调试中的问题和解决过程, 四个问题加4分 -
本周结对学习情况
-
上周博客互评情况
其他
这周的教材学习比较容易,所以花的时间相对较少,但是实验令人难受。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 8/8 | |
| 第二周 | 470/470 | 1/2 | 12/20 | |
| 第三周 | 685/1155 | 2/4 | 10/30 | |
| 第四周 | 2499/3654 | 2/6 | 12/42 | |
| 第六周 | 1218/4872 | 2/8 | 10/52 | |
| 第七周 | 590/5462 | 1/9 | 12/64 | |
| 第八周 | 993/6455 | 1/10 | 12/76 | |
| 第九周 | 1192/7467 | 2/12 | 10/86 |