正交排列法
说明:
正交表:数学---统计学的研究成果
使用最少的抽样数据达到最广的,覆盖率最高的统计结果
测试人员:需要选择合适的正交表,并且能将正交表应用到测试中即可
提示:正交表对于测试人员只是工具,不需要深入研究原理,也无需背诵。
一、 正交排列法的使用场合
在一个界面中有多个控件,每个控件有多个取值,测试要考虑不同控件不同取值之间的组合 ,但是组合数量较大(>20种,20种以下一般用因果图/判定表),没有必要全部测试,如何从所有组合中挑选最少的组合测试,并能得到最优的测试效果—使用正交排列法。
二.正交排列法和判定表法的主要异同:
1、都是用来测控件的组合问题
2、判定表法适合测组合数量较少的情况
3、正交排列法适合测组合数量较多的情况
4、判定表(因果图)会反映控件之间的限制和组合关系
5、正交排列表只需反映控件之间的组合关系。
三、解析正交表公式
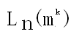
L:line 行
n:表示正交表有几行,需要测试的组合的个数
n值是固定的,一旦正交表确定n值就是固定的,不需要测试人员自己计算。
m:表示正交表中允许出现的最大值
根据每个控件的取值个数来确定m值
k:表示正交表有几列
根据组合的控件个数进行确定
四、使用正交表测试的步骤:
步骤1:分析需求--- 列出需要组合的控件以及每个控件的取值(excel)
步骤2:选择一个合适的正交表
选择正交表,其实就是确定正交表的m值和k值的过程
M(控件的取值个数):3
K(控件个数):4
正交表:3的4次幂
步骤3:应用正交表
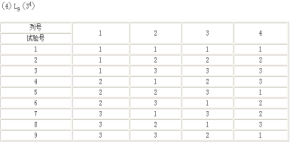
1、 把控件替换了正交表的列标题(因子)
2、 将每个控件的取值分别替换掉了对应正交表列的值(状态)
3、 应用正交表
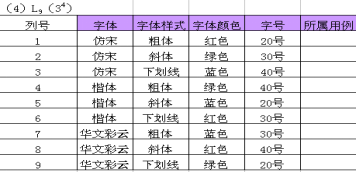
步骤4:根据正交排列表填写测试用例
把正交表中的1行编写1条测试用例,测试一种组合
说明:实际工作中有时会直接使用正交排列表测试,不写测试用例
五、关于正交排列法的总结
1、正交表是采用最少的测试数据,达到最优的测试效果,但是遗漏的组合较多。有遗漏缺陷的风险,如果时间允许,可以适当的补充测试
2、正交表法的局限:
1)正交表的个数有限(9个)
2)要求每个控件中的取值个数要相等,这在实际应用中很少遇到
3、正交表的特性:
1)每列中不同数值出现的次数均等
2)在任意两列中,同一行的两个数值组成有序数对,则有序数对出现的次数是均等的
六、正交表的强化操作—没有合适的正交表
1、控件的个数(k值)不符合
方案:选择最接近的但是稍微大一点的k值,用不到的列可以删掉
练习2:理论上:3的3次幂,但是没有正合适的正交表
最终选择:3的4次幂
2、没有合适的m值,怎么解决(powerpoint 软件的打印功能)
方法1:少数服从多数原则
M值相同的控件个数最多的那个m值
案例:分析结果,3的4次幂
方法2:最大值原则—选择控件取值个数最多的值当m值
案例分析:m=4(取值最大),k=4
理论上:4的4次幂,但是没有
最终选择:4的5次幂,多余1列可以删掉
方法总结:
1、 如果有多余的列,可以删除掉
2、 能映射的值先映射好(替换)
3、 把每一列多出的机会,尽量均匀分配给该列的各个取值
4、 要检查是否有完全一样的组合,如果有要适当处理(建议修改,也可以删除)
5、 选择正交表时正好能应用正交表示首选,如果不合适呢么选择最接近的。
实际工作中,属性设置测试,兼容性测试常用正交排列法,而且兼容性测试可以不编写测试用例,直接用正交排列表测试各种兼容组合。
可以看看这个的案例哦:https://www.cnblogs.com/fuxinxin/p/8991703.html