P4098 [HEOI2013]ALO

传送门

注意到关于次大值的要求，感觉直接搞不太行

考虑每个位置作为次大值时，可以包括的区间

设位置 $i$ 左边第一个大于它的数位置为 $l1$ ，第二个大于它的数位置为 $l2$

设位置 $i$ 右边第一个大于它的数位置为 $r1$ ，第二个大于它的数位置为 $r2$

如图所示：

 那么我们可以最多可以选择的区间就是这样：

 或者这样：

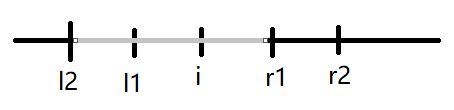
 所以对于每个位置 $i$ ，它可以和 $(l2,r2)$ 之间的任何一个数异或，并且由图显然，它不能和 $[1,l2]$ 或 $[r2,n]$ 的任何一个数异或

那么只要能知道每个位置的 $l2,r2$，我们就可以用可持久化 $01trie$ 直接求最大异或值

至于求 $l2,r2$ 的问题，我们可以把所有数从大到小排序一个个加入 $set$，这样每个数加入之前 $set$ 里的所有数都比它大，直接前驱后继走走即可

当然要特判一下 $set$ 里不存在 $l2,r2$ 的情况

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<set>
using namespace std;
typedef long long ll;
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
    return x*f;
}
const int N=5e4+7,M=33,MN=3e7;
int n,ans;
struct dat {
    int v,pos;
    inline bool operator < (const dat &tmp) const {
        return pos<tmp.pos;
    }
}d[N];
inline bool cmp(const dat &A,const dat &B) { return A.v>B.v; }
struct Trie {
    int rt[N],ch[MN][2],sz[MN],cnt=0;
    void insert(int &o,int d,int v,int pre)
    {
        o=++cnt; sz[o]=sz[pre]+1;
        if(d<0) return;
        int p=(v>>d)&1;
        insert(ch[o][p],d-1,v,ch[pre][p]);
        ch[o][p^1]=ch[pre][p^1];
    }
    int query(int o,int d,int v,int pre)
    {
        if(d<0) return 0;
        int p=((v>>d)&1)^1;
        if(sz[ch[o][p]]-sz[ch[pre][p]]) return (1<<d)|query(ch[o][p],d-1,v,ch[pre][p]);
        return query(ch[o][p^1],d-1,v,ch[pre][p^1]);
    }
}T;
set <dat> S;
set <dat>::iterator l,r;
int main()
{
    n=read();
    for(int i=1;i<=n;i++)
    {
        d[i].v=read(),d[i].pos=i;
        T.insert(T.rt[i],30,d[i].v,T.rt[i-1]);
    }
    sort(d+1,d+n+1,cmp); S.insert(d[1]);
    int L,R;
    for(int i=2;i<=n;i++)
    {
        l=r=S.lower_bound(d[i]);
        if(l!=S.begin()) l--;
        if(l!=S.begin()) l--,L=(*l).pos+1;
        else L=1;
        if(r!=S.end()) r++;
        if(r!=S.end()) R=(*r).pos-1;
        else R=n;
        ans=max(ans,T.query(T.rt[R],30,d[i].v,T.rt[L-1]));
        S.insert(d[i]);
    }
    printf("%d
",ans);
    return 0;
}