Codeforces886(Technocup2018) F Symmetric Projections
You are given a set of n points on the plane. A line containing the origin is called good, if projection of the given set to this line forms a symmetric multiset of points. Find the total number of good lines.
Multiset is a set where equal elements are allowed.
Multiset is called symmetric, if there is a point P on the plane such that the multiset is centrally symmetric in respect of point P.
Input
The first line contains a single integer (n (1 ≤ n ≤ 2000)) — the number of points in the set.
Each of the next n lines contains two integers (x_i) and (y_i) (( - 10^6 ≤ x_i, y_i ≤ 10^6)) — the coordinates of the points. It is guaranteed that no two points coincide.
Output
If there are infinitely many good lines, print -1.
Otherwise, print single integer — the number of good lines.
Examples
input
3
1 2
2 1
3 3
output
3
input
2
4 3
1 2
output
-1
Note
Picture to the first sample test:
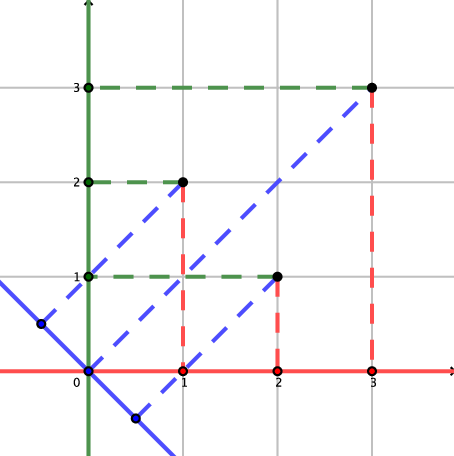
In the second sample, any line containing the origin is good.
题意描述
在平面上给出2000个点,求有多少条过原点的直线, 使这些点在直线上的投影对称
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
题解
(因为精度问题没过)
质心是所有点的平均坐标
???质心在合法的直线上的投影是对称重心???
假设两点是对称的, 那么他们的中点的投影必然是对称中心, 结合质心的性质, 这样可以唯一确定一条过原点的直线
注意到任意一点一定有投影后对称的点, 可能是自己, 所以只要随便拿一个点和(n)个点枚举就可以得到所有的可能直线, 即(O(n))
判断直线可不可行有很多方式