FJUT seventh的tired树上路径（01字典树）题解

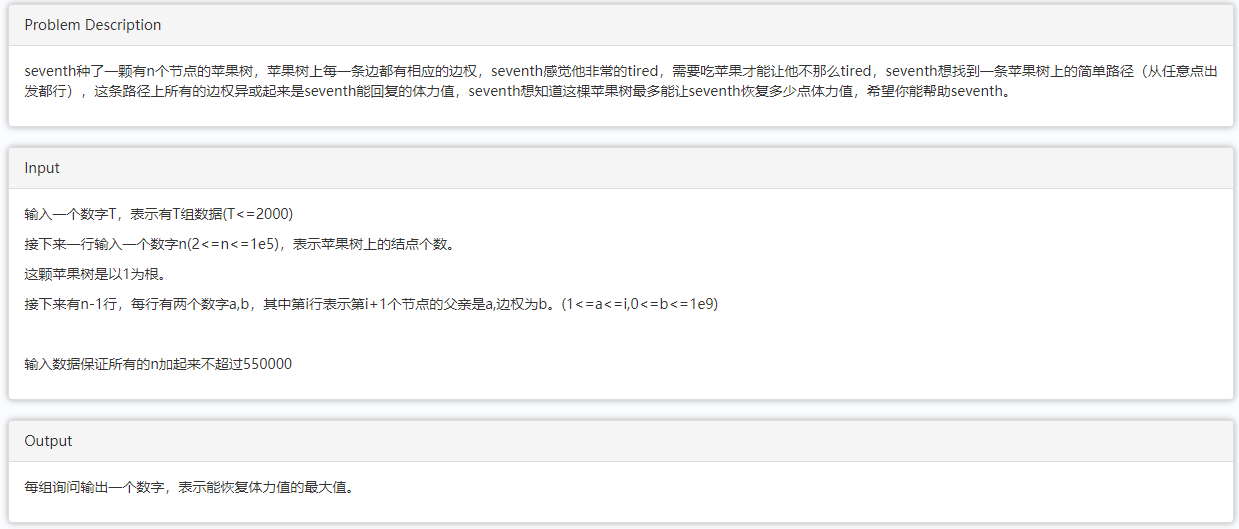
思路（来自题解）：

众所周知树上两个点xy的距离是deep[x]+deep[y]-deep[lca(x,y)]*2

然后我们把这个加减法换成异或，我们就会发现，deep[lca(x,y)]被消掉了

所以题目就简化成w是每个点的前缀异或和，只要找到一对最大的(x,y)让w[x]^w[y]最大就行了,这个经典问题用字典树就能解决了。

代码：

#include<set>
#include<map>
#include<stack>
#include<cmath>
#include<queue>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
typedef long long ll;
const int maxn = 1e5 + 10;
const int seed = 131;
const ll MOD = 1e9 + 7;
const ll INF = 1e17;
using namespace std;

int tol, node[32 * maxn][2];
ll val[32 * maxn], w[maxn];
void Insert(ll x){
    int root = 0;
    for(int i = 31; i >= 0; i--){
        int u = (x >> i) & 1;
        if(node[root][u] == 0){
            memset(node[tol], 0, sizeof(node[tol]));
            node[root][u] = tol++;
        }
        root = node[root][u];
    }
    val[root] = x;
}
ll query(ll x){
    int root = 0;
    for(int i = 31; i >= 0; i--){
        int u = (x >> i) & 1;
        if(node[root][!u])
            root = node[root][!u];
        else root = node[root][u];
    }
    return x ^ val[root];
}
int main(){
    int T, n, a;
    ll x;
    scanf("%d", &T);
    while(T--){
        memset(node[0], 0, sizeof(node[0]));
        tol = 1;
        w[1] = 0;
        scanf("%d", &n);
        for(int i = 2; i <= n; i++){
            scanf("%d%lld", &a, &x);
            w[i] = x ^ w[a];
            Insert(w[i]);
        }
        ll ans = 0;
        for(int i = 1; i <= n; i++){
            ans = max(ans, query(w[i]));
        }
        printf("%lld
", ans);
    }
    return 0;
}