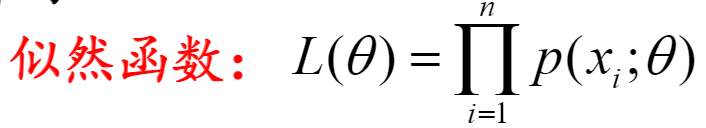概率论与数理统计

1. 相互独立：P(AB)=P(A)P(B)

2. 分布函数F(X)，概率密度f(x)

f(x)求积分后是F(x)

3. 常用分布：0-1分布，二项分布，超几何分布，泊松分布，均匀分布，指数分布，正态分布

4. 随机变量数学期望E(X)= xf(x)求积分

方差D(X)=E{ [X-E(X)]^2 }

协方差cov(X,Y)=E{ [X-E(X)][Y-E(Y)] }

相关系数=cov(X,Y) / 根号下D(X)D(Y)

5. 大数定律：当n趋近无穷时，Xn与常数A的差始终很小可忽略，则认为该随机变量序列依概率收敛于A

中心极限定理：n个随机变量独立同分布，已知其期望和方差，可以认为其近似服从一个正态分布N(nu,no^2)。

6. 统计抽样分布：

卡方分布：对一个标准正态分布，随机变量 卡方=X1^2+...+Xn^2

t分布：对一个标准正态和一个卡方分布，随机变量T=X / 根号下Y/n

F分布：两个卡方分布，随机变量F=(X/n1)/(Y/n2)

7. 估计的目的是把分布里的参数估计出来

点估计：猜一个数；区间估计：猜一个区间

矩估计：

极大似然估计：求出似然函数取极大值时，对应参数的值为估计值