游戏中的一些数学物理问题（1）

最近在做一个游戏，愤怒小鸟百战天虫一类的，好像叫做炮术游戏吧。然后遇到了一些数学问题，发现自己果然不擅长数学，花了不少时间。分享一下已经解决的问题。

已实现的内容：人物的初速度根据触点离人物位置而变化，触点离人物越远，松手后人物的初速度越大，飞的越远

问题：因为人物不能无限飞行。

 

需求：限制人物的行动范围。

 

要限制人物的行动范围，比较好的实现方法是限制人物的最大初始速度，也就是限制触点所能赋予玩家的最大速度。

最早的代码如下：

 

var touchX = event.getLocationX();
var touchY = event.getLocationY();
var canvasX = 1280, canvasY = 736;

var moveX = touchX - (this.player.x + 0.5 * canvasX);
var moveY = touchY - (this.player.y + 0.5 * canvasY);
           
//半径
var radius = 50;
if(moveX > radius){
    moveX = radius;
} else if(moveX > -radius) {
    moveX = -radius;
}
if(moveY > radius){
    moveY = radius;
} else if(moveY > -radius) {
    moveY = -radius;
}

this.speed = cc.v2(-moveX*0.3, -moveY*0.3);

代码中moveX、moveY是触点相对于人物的坐标，通过这种方法限制moveX、moveY的最大值。但是这段代码的运行效果是把moveX、moveY的范围限制在一个边长为2radius的正方形范围内。正方形限制显然是不合理的，在正方形的边缘上各个点获得的初速度参差不齐，在正方形的顶点获得的初速度大得夸张。

 

理想的效果是把moveX、moveY限制在一个固定半径的圆内。这需要用到中学的数学知识，圆锥曲线。通过百度得到圆函数：圆的标准方程 (x-a)²+(y-b)²=r²  方程中的a、b是圆心坐标，我们以玩家中心(0,0)为圆心所以我们要用到的是x²+y²=r²。

 

还要用到三角函数，因为本质上是通过限制x,y的速度在x,y轴上的投影来限制x,y的坐标的，理解这点很重要。

 

 

 

 

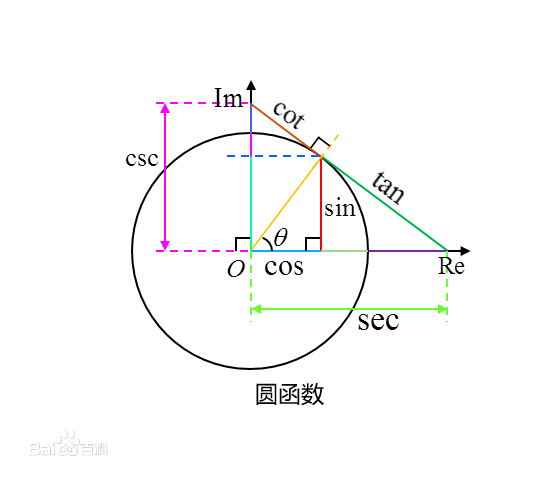
写代码的时候被图片误导了，而且当时对圆方程的理解也欠缺，错误的代码：var sinAngle = moveY/radius; 一开是用半径求三角函数，在图片上来看这样是正确的，但是实际过程中的三角函数值不能用半径来求，因为触碰屏幕时触点所在的圆并不在那个固定半径的圆上。所在的圆的半径是   #根号（x²+y²）#  通过坐标来动态求正弦余弦。

 

var touchX = event.getLocationX();
var touchY = event.getLocationY();
var canvasX = 1280, canvasY = 736;

var moveX = touchX - (this.player.x + 0.5 * canvasX);
var moveY = touchY - (this.player.y + 0.5 * canvasY);


//半径，正弦，余弦
var radius = 50;
var sinAngle = moveY/Math.sqrt(Math.pow(moveX,2)+Math.pow(moveY,2));
var cosAngel = moveX/Math.sqrt(Math.pow(moveX,2)+Math.pow(moveY,2));

if(Math.sqrt(Math.pow(moveX,2)+Math.pow(moveY,2)) >= radius){
    moveX = cosAngel*radius;
    moveY = sinAngle*radius;
}

this.speed = cc.v2(-moveX*0.3, -moveY*0.3);

最终实现效果：