题意:给出第一象限的N个点,存在一直线x/a+y/b=1(a>0,y>0)使得所有点都在这条直线下面,求 min{sqrt(a^2+b^2)}
显然,这样的直线必然经过这N个点中的某一个(可用反证法证得),所以先对只有一个点的情况进行分析。
当只有一个点P(x0,y0)时,易得
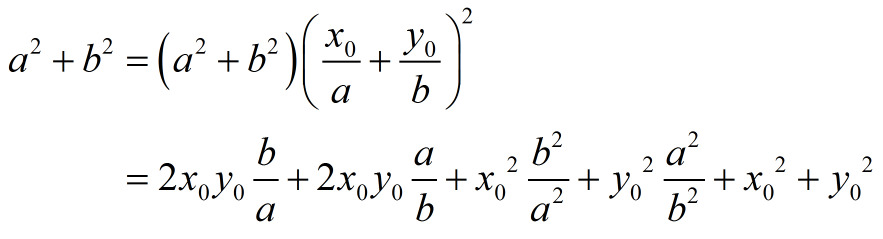
此时设t=a/b,可知,a^2+b^2可写成两个凹函数相加的形式,故可用三分法求解。
所以N个点的情况就可解了。容易想到,只需要考虑凸包上位于右上侧的点(满足该点的左上方右下方都有点),那么该点就有成为“关键的点”的可能,至于三分时的自变量的范围,就根据这个点的前后两个点来得到即可。
#include<bits/stdc++.h> using namespace std; const double eps=1e-9; const double inf=2e6; int dcmp(double x) { if(fabs(x)<eps) return 0; else return x<0? -1:1; } struct Point { double x,y; Point(double x_=0,double y_=0) { x=x_,y=y_; } Point operator -(const Point& rhs) { return Point(x-rhs.x,y-rhs.y); } bool operator<(const Point& rhs)const { return x<rhs.x||x==rhs.x&&y<rhs.y; } }; typedef Point Vector; double Cross(Vector A,Vector B) { return A.x*B.y-A.y*B.x; } double Area2(Point A,Point B,Point C) { return Cross(B-A,C-A); } int ConvexHull(Point *p,int n,Point *ch) { sort(p,p+n); int m=0; for(int i=0; i<n; i++) { while(m>1&&dcmp(Area2(ch[m-2],ch[m-1],p[i]))<=0) --m; ch[m++]=p[i]; } int k=m; for(int i=n-2; i>=0; --i) { while(m>k&&dcmp(Area2(ch[m-2],ch[m-1],p[i]))<=0) --m; ch[m++]=p[i]; } return n>1? m-1:m; } //============================================================= const int maxn=1e6+5; Point p[maxn],ch[maxn]; double k[maxn]; double xielv(Point A,Point B) { if(dcmp(A.x-B.x)==0) return -inf; else return (A.y-B.y)/(A.x-B.x); } double cal(Point P,double P_k) { double a=P.x-P.y/P_k; double b=P.y-P.x*P_k; return sqrt(a*a+b*b); } double sanfen(Point P,double k1,double k2) { double l=k1,r=k2; while(r-l>eps) { double mid=(l+r)/2; double f1=cal(P,mid); double midmid=(mid+r)/2; double f2=cal(P,midmid); if(f1<f2) r=midmid; else l=mid; } return cal(P,l); } int main() { int n,m; while(~scanf("%d",&n)) { double ans=inf; double maxx=0,maxy=0; for(int i=0; i<n; i++) //读点 { scanf("%lf%lf",&p[i].x,&p[i].y); maxx=max(maxx,p[i].x),maxy=max(maxy,p[i].y); } p[n++]=Point(maxx,0),p[n++]=Point(0,maxy); //加点,便于处理 m=ConvexHull(p,n,ch); //求凸包 for(int i=0; i<m; i++) k[i]=xielv(ch[i],ch[(i+1)%m]); //求斜率 for(int i=0; i<m; i++) if(ch[i].x>=ch[(i+1)%m].x&&ch[i].y<=ch[(i+1)%m].y && ch[(i+1)%m].x>=ch[(i+2)%m].x&&ch[(i+1)%m].y<=ch[(i+2)%m].y) ans=min(ans,sanfen(ch[(i+1)%m],k[i],k[(i+1)%m])); printf("%.3lf ",ans+eps); } }