定义:
-
排列组合是组合学最基本的概念。所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。
-
排列的定义:从n个不同元素中,任取m(m≤n,m与n均为自然数,下同)个元素按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列;从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号 A(n,m)表示。此外规定0!=1(n!表示n(n-1)(n-2)...1,也就是6!=6x5x4x3x2x1
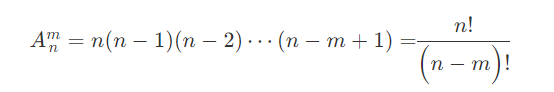
- 组合的定义:从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合;从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数。用符号 C(n,m) 表示。
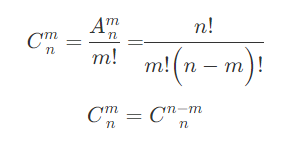
代码:
#include "bits/stdc++"
using namespace std;
int factorial(int n);
int Arrangement(int n, int m);
int Combination(int n, int m);
const int SIZE = 40;
int main()
{
printf("输入全数n和选数m:");
int n, m;
cin >> n >> m;
printf("n的阶乘为:%d; m的阶乘为:%d; n和m的排列为:%d; n和m的组合为:%d.", factorial(n), factorial(m), Arrangement(n, m), Combination(n, m));
_getch();
return 0;
}
int factorial(int n)
{
int sum = 1;
return n == 1 ? sum = 1 : n * factorial(n - 1);
}
int Arrangement(int n, int m)
{
return factorial(n) / factorial(n - m);
}
int Combination(int n, int m)
{
return factorial(n) / factorial(m) * factorial(n - m);
}