P1396 营救【DFS+二分 kruskal】

题目

https://www.luogu.com.cn/problem/P1396

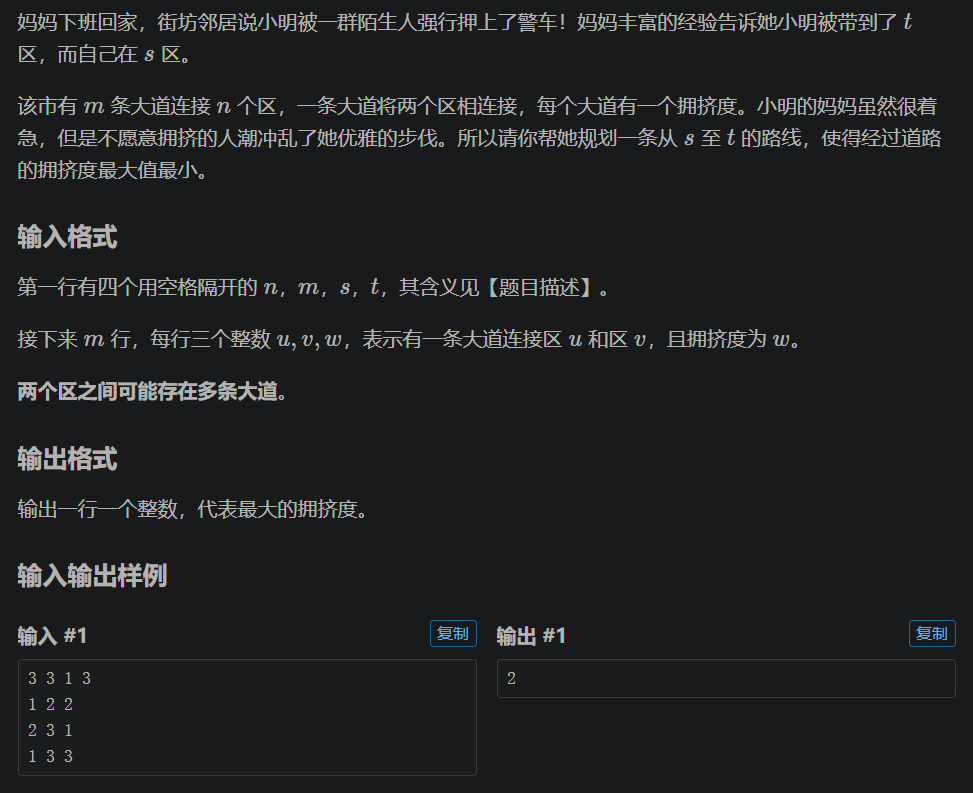
 分析

这道题与这道题很相似，只不过那道题需要使用dijkstra判断是否到达，而本题只需要使用DFS来判断

大概思路就是这种最大值中的最小的问题：

先找到题目中用到的拥挤度的最大值以及最小值，然后在这个范围内进行二分搜索，在每一次的搜索中，我们使用dfs看以本次搜索用的拥挤度为最大值看在不超过该值的情况下能否从S点到达T点

能的话就缩小二分搜索的值继续查找，如果不能就把搜索的值改大一点，继续搜索

代码

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
using namespace std;
#define maxn 10003
#define maxm 2*maxn
#define inf 0x3f3f3f3f
struct node
{
    int to;
    int next;
    int dis;
}e[maxm*2];
int cnt = 0,n,m,s,t;
int head[maxn],vis[maxn];
void addedge(int u, int v, int w)
{
    cnt++;
    e[cnt].dis = w;
    e[cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt;
}
bool ok = false;
void dfs(int start,int cost)
{

    if (start == t)ok = true;
    vis[start] = 1;
    for (int i = head[start]; i; i = e[i].next)
    {
        int y = e[i].to;
        if (vis[y])continue;
        if (e[i].dis > cost)continue;
        dfs(y,cost);
    }
}

int main()
{
    scanf("%d%d%d%d", &n, &m, &s, &t);
    int maxx = -1;
    int minn = inf;
    for (int i = 1; i <= m; i++)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        if (maxx < c)maxx = c;
        if (minn > c)minn = c;
        addedge(a, b, c);
        addedge(b, a, c);
    }
    int l = minn, r = maxx;
    int ans = 0;
    while (l <= r)
    {
        memset(vis, 0, sizeof(vis));
        ok = false;
        int mid = (l + r) / 2;
        dfs(s, mid);
        if (ok) { r = mid - 1; ans = mid; }
        else l = mid + 1;
    }
    printf("%d", ans);
}

该题的思路还可以使用kruskal算法，在寻找最小生成树的过程中，一旦发现S点与T点已经连接到了一起，就输出此时的边值，因为在寻找的过程中边值的大小是从小到大排列的

所以最后输出的一定是最大的也就是最大值中的最小（其实是先使用kruskal实现最小，再在最小里找最大）而上面的方法是在保证最大的条件下找最小

代码

#include<iostream>
#include<cstdio>
#include<string>
#include<algorithm>
#include<cstring>
using namespace std;
#define maxn 20001
#define maxm 2*maxn
#define inf 0x3f3f3f3f
struct node
{
    int from;
    int to;
    int dis;
}e[maxm * 2];
int cnt = 0, n, m, s, t;
int father[maxn];
bool cmp(struct node&a, struct node &b)
{
    return a.dis < b.dis;
}
int find(int x)
{
    if (x == father[x])return x;
    return father[x] = find(father[x]);
}
int kruskal()
{
    sort(e, e + m, cmp);
    for (int i = 0; i < m; i++)
    {
        int tempx = find(e[i].from);
        int tempy = find(e[i].to);
        if (tempx == tempy)continue;
        father[tempx] = tempy;
        if (find(s) == find(t))
        {
            return e[i].dis;
        }
    }
}

int main()
{
    scanf("%d%d%d%d", &n, &m, &s, &t);
    for (int i = 0; i < m; i++)
        scanf("%d%d%d", &e[i].from, &e[i].to, &e[i].dis);
    for (int i = 0; i <= m; i++)
        father[i] = i;
    
    printf("%d", kruskal());

}