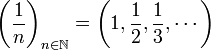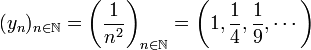1. 子序列
摘自维基百科
在数学中,某个序列的子序列是从最初序列通过去除某些元素但不破坏余下元素的相对位置而形成的新序列。
例如:
令  为一序列
为一序列
那么,以下序列
是  的子序列之一。对应定义里的自然数子序列
的子序列之一。对应定义里的自然数子序列 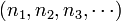 为
为 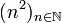 ,而所对应的映射函数为
,而所对应的映射函数为  。
。
2. 最长公共子序列
最长公共子序列问题是寻找两个或多个已知数列最长的子序列
3. 解题思路
最长公共子序列的性质:
设序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列为Z={z1,z2,…,zk} ,则
(1)若xm=yn,则zk=xm=yn,且{z1...zk-1}是{x1...xm-1}和{y1...yn-1 }的最长公共子序列。
(2)若xm≠yn且zk≠xm,则{z1....zk } 是{x1...xm-1}和{y1....yn}最长公共子序列。
(3)若xm≠yn且zk≠yn,则{z1...zk}是{x1...xm}和{y1...yn-1}的最长公共子序列。
则可以有如下的递归关系:
c[i][j]表示x的第i位和y的第j位之前(包括i和j)的最长公共子序列的个数
因此在求解的时候也分为这三种情况来考虑即可。
最后还要用回溯的方法把最长子串输出出来,详细的方法可以参考:http://blog.csdn.net/yysdsyl/article/details/4226630 他已经写得很清楚了。
4. 代码
//LCS longest common subsequence #include <stdio.h> #include <stdlib.h> #include <string.h> #define MAX 100 void LCS(char *x, char *y,int x_len, int y_len, int common_len[][MAX], int b[][MAX]) { //common_len[i][j]存储的是x的第i位与有的第j位的公共子序列的长度 //b[i][j] 记录获得common_len[i][j]的路径:分别为0 -1 1,便于回溯输出公共子串 int i,j; for (i = 0; i < x_len; i++) common_len[i][0] = 0; for (j = 0; j < y_len; j++) common_len[0][j] =0; for (i = 1; i <= x_len; i++) { for (j = 1; j <= y_len; j++) { if (x[i-1] == y[j-1]) //从零开始存储,所以第i位为x[i-1] { common_len[i][j] = common_len[i-1][j-1] + 1; b[i][j] = 0; } else if (common_len[i-1][j] >= common_len[i][j-1]) { common_len[i][j] = common_len[i-1][j]; b[i][j] = -1; } else { common_len[i][j] = common_len[i][j-1]; b[i][j] = 1; } } } } void backtrack(int i, int j,int b[][MAX], char *x) { if (0 == i || 0 == j) return; else if (0 == b[i][j]) { backtrack(i-1,j-1,b,x); printf("%c",x[i-1]); } else if(-1 == b[i][j]) { backtrack(i-1,j,b,x); } else { backtrack(i,j-1,b,x); } } int main() { int x_len,y_len; char x[MAX] = "ABCBDAB"; char y[MAX] = "BDCABA"; int common_len[MAX][MAX]; int b[MAX][MAX]; x_len = strlen(x); y_len = strlen(y); LCS(x,y,x_len,y_len,common_len,b); backtrack(x_len,y_len,b,x); printf(" "); return 0; }
2013/8/8 11:27
接下来,要做的就是深入学习动态规划和回溯的问题