[NOIP2014]联合权值

题目描述

无向连通图G 有n 个点，n - 1 条边。点从1 到n 依次编号，编号为 i 的点的权值为W i ，每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ，若它们的距离为2 ，则它们之间会产生Wu×Wv 的联合权值。

请问图G 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入输出格式

输入格式：

输入文件名为link .in。

第一行包含1 个整数n 。

接下来n - 1 行，每行包含 2 个用空格隔开的正整数u 、v ，表示编号为 u 和编号为v 的点之间有边相连。

最后1 行，包含 n 个正整数，每两个正整数之间用一个空格隔开，其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。

输出格式：

输出文件名为link .out 。

输出共1 行，包含2 个整数，之间用一个空格隔开，依次为图G 上联合权值的最大值

和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对10007 取余。

输入输出样例

输入样例#1：

5  
1 2  
2 3
3 4  
4 5  
1 5 2 3 10 

输出样例#1：

20 74

说明

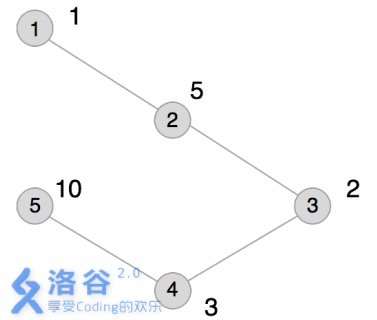
本例输入的图如上所示，距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30% 的数据，1 < n≤ 100 ；

对于60% 的数据，1 < n≤ 2000；

对于100%的数据，1 < n≤ 200 , 000 ，0 < wi≤ 10, 000 。

思路

过某点的最大联合权值为所有与该点相连的点中最大点权与次大点权的乘积；

过该点的最大联合权值之和为所有与该点相连的点的点权的和的平方减去平方的和；

代码实现

#include<cstdio>
const int maxn=1e6;
const int mod=10007;
inline int max_(int x,int y){return x>y?x:y;}
int n,max,mbx,num,tot,mmax,tota;
int a,b;
int s[maxn];
int h[maxn],hs;
int e_s[maxn],e_n[maxn];
int main(){
    scanf("%d",&n);
    for(int i=1;i<n;i++){
        scanf("%d%d",&a,&b);
        ++hs,e_s[hs]=b,e_n[hs]=h[a],h[a]=hs;
        ++hs,e_s[hs]=a,e_n[hs]=h[b],h[b]=hs;
    }
    for(int i=1;i<=n;i++) scanf("%d",&s[i]);
    for(int i=1;i<=n;i++){
        max=mbx=num=tot=0;
        for(int j=h[i];j;j=e_n[j]){
            if(s[e_s[j]]>mbx){
                mbx=s[e_s[j]];
                if(mbx>max) max^=mbx,mbx^=max,max^=mbx;
            }
            tot=(tot+(s[e_s[j]]*s[e_s[j]])%mod)%mod;
            num=(num+s[e_s[j]])%mod;
        }
        mmax=max_(mmax,max*mbx);
        tota=(tota+(num*num-tot)%mod)%mod;
    }
    printf("%d %d
",mmax,tota);
    return 0;
}

要完成这道题目，我们需要高深的数学知识，比如乘法分配律什么的。。。