题目描述
C 国有 n 个大城市和 m 条道路,每条道路连接这 n 个城市中的某两个城市。任意两个
城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路,一部分
为双向通行的道路,双向通行的道路在统计条数时也计为 1 条。
C 国幅员辽阔,各地的资源分布情况各不相同,这就导致了同一种商品在不同城市的价
格不一定相同。但是,同一种商品在同一个城市的买入价和卖出价始终是相同的。
商人阿龙来到 C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息
之后,便决定在旅游的同时,利用商品在不同城市中的差价赚回一点旅费。设 C 国 n 个城
市的标号从 1~ n,阿龙决定从 1 号城市出发,并最终在 n 号城市结束自己的旅行。在旅游的
过程中,任何城市可以重复经过多次,但不要求经过所有 n 个城市。阿龙通过这样的贸易方
式赚取旅费:他会选择一个经过的城市买入他最喜欢的商品――水晶球,并在之后经过的另
一个城市卖出这个水晶球,用赚取的差价当做旅费。由于阿龙主要是来 C 国旅游,他决定
这个贸易只进行最多一次,当然,在赚不到差价的情况下他就无需进行贸易。
假设 C 国有 5 个大城市,城市的编号和道路连接情况如下图,单向箭头表示这条道路
为单向通行,双向箭头表示这条道路为双向通行。
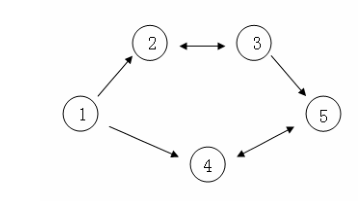
假设 1~n 号城市的水晶球价格分别为 4,3,5,6,1。
阿龙可以选择如下一条线路:1->2->3->5,并在 2 号城市以 3 的价格买入水晶球,在 3
号城市以 5 的价格卖出水晶球,赚取的旅费数为 2。
阿龙也可以选择如下一条线路 1->4->5->4->5,并在第 1 次到达 5 号城市时以 1 的价格
买入水晶球,在第 2 次到达 4 号城市时以 6 的价格卖出水晶球,赚取的旅费数为 5。
现在给出 n 个城市的水晶球价格,m 条道路的信息(每条道路所连接的两个城市的编号
以及该条道路的通行情况)。请你告诉阿龙,他最多能赚取多少旅费。
输入输出格式
输入格式:
第一行包含 2 个正整数 n 和 m,中间用一个空格隔开,分别表示城市的数目和道路的
数目。
第二行 n 个正整数,每两个整数之间用一个空格隔开,按标号顺序分别表示这 n 个城
市的商品价格。
接下来 m 行,每行有 3 个正整数,x,y,z,每两个整数之间用一个空格隔开。如果 z=1,
表示这条道路是城市 x 到城市 y 之间的单向道路;如果 z=2,表示这条道路为城市 x 和城市
y 之间的双向道路。
输出格式:
输出文件 trade.out 共 1 行,包含 1 个整数,表示最多能赚取的旅费。如果没有进行贸易,
则输出 0。
输入输出样例
5 5 4 3 5 6 1 1 2 1 1 4 1 2 3 2 3 5 1 4 5 2
5
说明
【数据范围】
输入数据保证 1 号城市可以到达 n 号城市。
对于 10%的数据,1≤n≤6。
对于 30%的数据,1≤n≤100。
对于 50%的数据,不存在一条旅游路线,可以从一个城市出发,再回到这个城市。
对于 100%的数据,1≤n≤100000,1≤m≤500000,1≤x,y≤n,1≤z≤2,1≤各城市
水晶球价格≤100。
NOIP 2009 提高组 第三题
思路:SPFA
建边,s(起点)一遍SPFA求出起点可以扩展到的点的最小值;
重新建边,t(终点)一遍SPFA求出终点可以扩展到的点的最大值;
遍历每个点,求出差值最值。
代码实现:
1 #include<cstdio> 2 #include<cstring> 3 const int maxn=1e5+10; 4 const int maxm=1e5*5+10; 5 int n,m,ans; 6 int a,b,c; 7 int s[maxn],q[maxn],z[maxn]; 8 int qe[maxm],head,tail; 9 int h[maxn],hs=1; 10 struct edge{int s,n;}e[maxm<<1]; 11 struct buid{int a,b,c;}r[maxm<<1]; 12 void add(int x,int y){e[++hs]=(edge){y,h[x]},h[x]=hs;} 13 inline int min_(int x,int y){return x<y?x:y;} 14 inline int max_(int x,int y){return x>y?x:y;} 15 int main(){ 16 scanf("%d%d",&n,&m); 17 for(int i=1;i<=n;i++) scanf("%d",&s[i]); 18 for(int i=1;i<=m;i++){ 19 scanf("%d%d%d",&r[i].a,&r[i].b,&r[i].c); 20 add(r[i].a,r[i].b); 21 if(r[i].c==2) add(r[i].b,r[i].a); 22 } 23 memset(q,0x7f,sizeof(q)); 24 q[1]=s[1],qe[head++]=1; 25 while(head>tail){ 26 a=qe[tail++]; 27 for(int i=h[a];i;i=e[i].n) 28 if(b=min_(q[a],s[e[i].s]),b<q[e[i].s]){ 29 qe[head++]=e[i].s; 30 q[e[i].s]=b; 31 } 32 } 33 memset(h,0,sizeof(h)); 34 head=tail=0,hs=1; 35 for(int i=1;i<=m;i++){ 36 add(r[i].b,r[i].a); 37 if(r[i].c==2) add(r[i].a,r[i].b); 38 } 39 z[n]=s[n],qe[head++]=n; 40 while(head>tail){ 41 a=qe[tail++]; 42 for(int i=h[a];i;i=e[i].n) 43 if(b=max_(z[a],s[e[i].s]),b>z[e[i].s]){ 44 qe[head++]=e[i].s; 45 z[e[i].s]=b; 46 } 47 } 48 for(int i=1;i<=n;i++) 49 ans=max_(ans,z[i]-q[i]); 50 printf("%d ",ans); 51 return 0; 52 }
一开始忘记重新建边了,没有一遍过。。。