模式识别的基本概念
- 模式识别:根据已有知识的表达,针对待识别模式,判别决策其所属的类别或者预测其对应的回归值。模式识别本质上是推理的过程。

- 数学表达:模式识别可以看做一种函数映射f(x),将待识别模式x从输入空间映射到输出空间。函数F(x)是关于已有知识的表达。
- 模型:已有知识的表达式y=f(x)。
- 模型的组成:特征提取+回归器
- 特征: 用于区分不同类别的、可观测的量,具有辨别能力和鲁棒性。
机器学习的基本概念
机器学习使用训练样本学习模型的参数和结构。模型结构分为线性结构和非线性结构。机器学习分为,无监督、半监督、监督式学习三种。

模型泛化能力
- 泛化能力指的是器学习方法训练出来一个模型,对于已知的数据(训练集)性能表现良好,对于未知的数据(测试集)也应该表现良好的机器能力。泛化能力低会导致过拟合,即在训练阶段表现良好在测试阶段表现很差。因此不要过度训练,或者引入正则项。
评估方法与性能指标
- 评估方法:留出法,K折交叉验证,留一验证。
- 性能指标:准确度:将阳性和阴性综合起来度量识别正确的程度。精度:预测为阳性样本的准确程度。召回率:全部阳性样本中被预测为阳性的比例。
基于距离的分类器
MED分类器
- 定义:把测试样本到每个类之前的距离作为决策模型,将测试样本判定为与其距离最近的类。
类的原型
- 概念:用来代表这个类的一个模式或者一组量,便于计算该类和测试样本之间的距离
[d(x,Ci)=d(y,Zi)
]
其中Zi表示类Ci的原型
原型的种类
均值
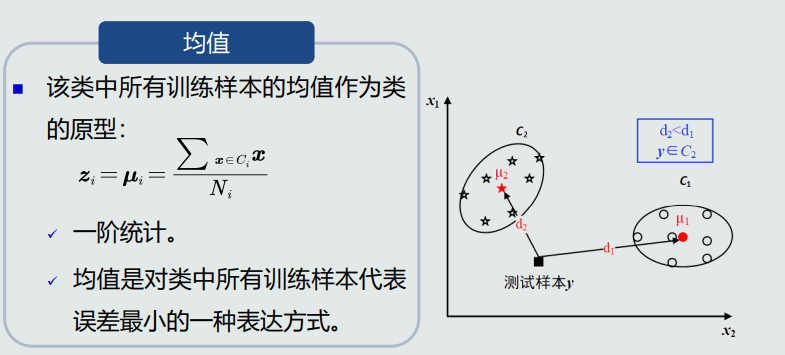
最近邻
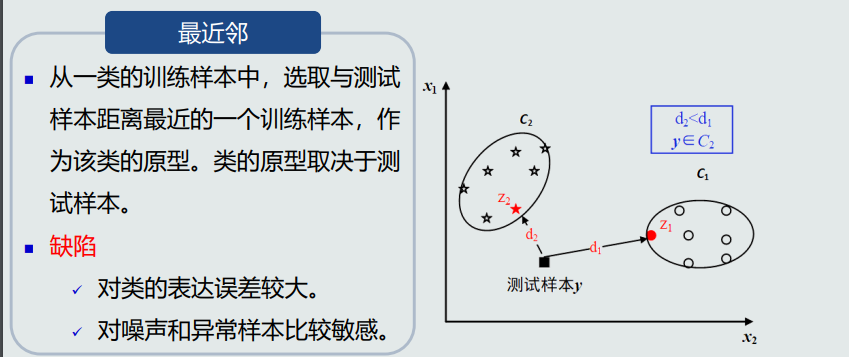
距离度量
方式:欧氏距离,曼哈顿距离,加权欧氏距离
MED分类器
概念:最小欧氏距离分类器。
- 距离衡量:欧氏距离
- 类的原型:均值
- 决策边界

特征白化
目的:去除特征变化的不同及特征之间的相关性。
- 特征正交白化


- 特征解耦

MICD分类器
概念:最小类内距离分类器,基于马氏距离的分类器。
- 判别公式

- 决策边界

贝叶斯决策与学习
贝叶斯决策与MAP分类器
- 后验概率:

- 贝叶斯规则:

- MAP分类器:
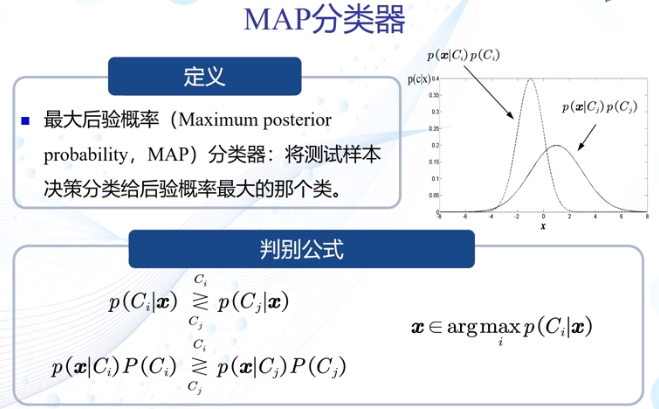
MAP分类器:高斯观测概率
- 观测概率:单维高斯分布

- 决策边界:

决策风险与贝叶斯分类器
- 决策风险和损失的概念
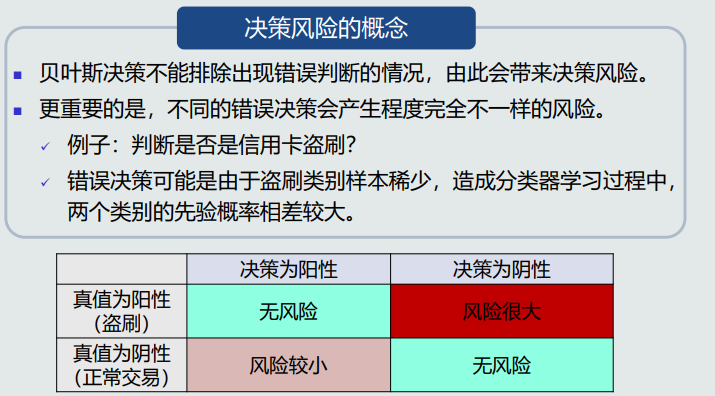

- 风险评估

贝叶斯分类器
在MAP分类器的基础上,加入决策风险因素。
- 朴素贝叶斯分类器

最大似然估计
定义

- 目标函数

- 均值

- 协方差

最大似然的估计偏差
- 高斯分布均值的最大似然估计是无偏估计,协方差的最大似然估计是有偏估计。
贝叶斯估计
概念

KNN估计

线性判据与回归
线性判据基本概念
生成模型

判别模型

线性判据学习概述
- 线性判据

- 学习和识别过程

如何找最优解
- 目标函数

并行感知机算法
- 算法流程

串行感知机算法
- 算法流程

Fisher线性判据
设计动机:线性判据的模型可以看做把原空间个点 x 投影到新的以为空间y
- 原理

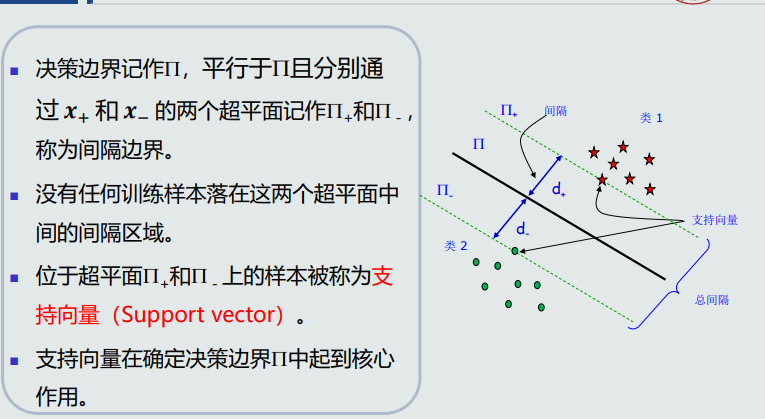
支持向量机基本概念
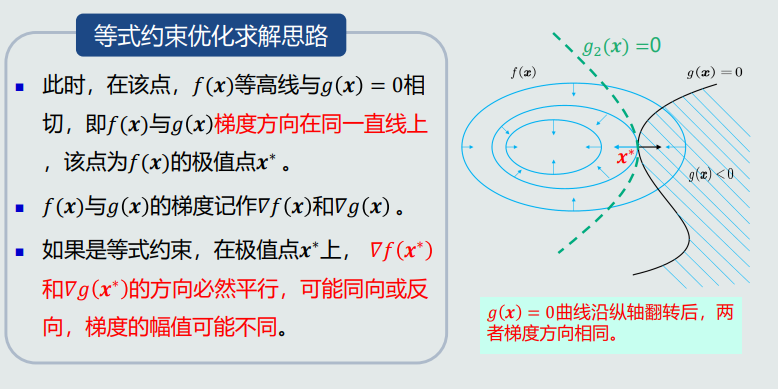
拉格朗日乘数法
- 等式约束

拉格朗日对偶问题
*对偶函数

支持向量机学习算法
算法过程
- 1构建拉格朗日函数

- 2构建对偶函数

决策过程
