排序算法

八大排序算法 详见http://blog.csdn.net/intheair100/article/details/48734563

http://blog.csdn.net/wangiijing/article/details/51485119

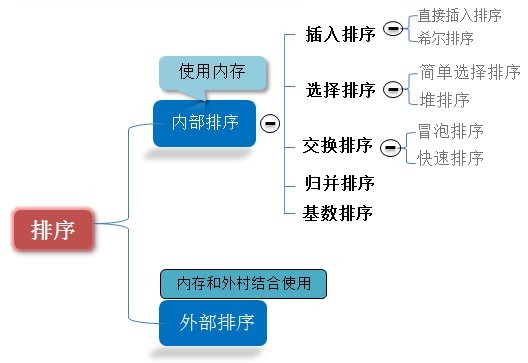
内部排序：在内存中，主要消耗时间复杂度，用比较次数衡量效率

外部排序：不断在内外存间移动，主要消耗空间复杂度，用读/写外村的次数来衡量效率

直接插入排序

 

java代码

public static void insertionSort(int[] arr) {
    for (int i = 1; i < arr.length; i++) {
        int j = i;
        while (j > 0 && arr[j] < arr[j - 1]) {
            swap(arr,j,j-1);
            j--;
        }
    }
}

最好的情况下，arr[j] 总是 不小于 arr[j-1]的，此时不执行while循环，所以此时时间复杂度为 O(n)

最坏的情况下，每次都执行while循环，所以此时时间复杂度为O(n^2)

平均时间复杂度是O(n^2)  ，空间复杂度为 O(1)，稳定

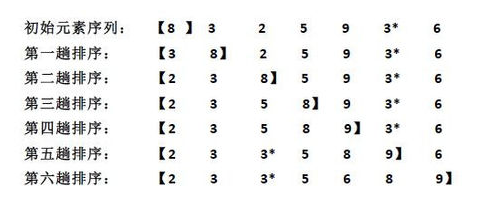
希尔排序

更清晰的图示见此。

初始元素序列            8 9 1 7 2 3 5 4 6 0

Step1(gap=n/2=5)： 3 5 1 6 0 8 9 4 7 2    因为此时有[8,3] [9,5] [1,4] [7,6] [2,0]对每组进行直接插入排序

Step2(gap=5/2=2)： 0 2 1 4 3 5 7 6 9 8    因为此时有[3,1,0,9,7] [5,6,8,4,2]

Step3(gap=2/2=1)： 0 1 2 3 4 5 6 7 8 9

    public static void sort(int []arr){
        //增量gap，并逐步缩小增量
       for(int gap=arr.length/2;gap>0;gap/=2){
           //从第gap个元素，逐个对其所在组进行直接插入排序操作
           for(int i=gap;i<arr.length;i++){
               int j = i;
               while(j-gap>=0 && arr[j]<arr[j-gap]){
                   //插入排序采用交换法
                   swap(arr,j,j-gap);
                   j-=gap;
               }
           }
       }
    }

最好的情况下，时间复杂度为 O(n)

最坏的情况下，时间复杂度为O(n^2)

平均时间复杂度是O(n^3/2)  ，空间复杂度为 O(1)，不稳定

简单选择排序

初始元素序列：    [ 49  38  65  97  76  13  27 ]   比较次数

第一趟           ：     13  [ 38  65  97  76  49  27 ]    n-1

第二趟           ：     13    27 [ 65  97  76  49  38 ]   n-2

第三趟           ：     13   27   38  [ 97 76  49  65 ]   n-3

第四趟           ：      13   27   38   49 [76  97 65 ]   n-4

第五趟           ：      13   27   38   49  65 [97  76]   n-5

第六趟           ：      13   27   38   49  65   76  97   n-6

详见此。

public void selectSort(int List[], int len)
{
    //简单选择排序的循环
    for (int i = 0; i < len; i++) {
        int k = i;
        //一次排序过程，终止条件是 j 扫描到了最后一个记录处
        for (int j = i + 1; j <= len; j++) {
            if (List[j] < List[k]) {
                k = j;
            }
        }
        //扫描完毕，交换最值，先判断是否重复
        if (i != k) {
            //交换
            List[i] = List[i] + List[k];
            List[k] = List[i] - List[k];
            List[i] = List[i] - List[k];
        }// end of if
    }//end of for
}

比较次数n(n-1)/2，不稳定

堆排序 

堆排序的步骤可以描述如下：

      1.构建大根堆。首先我们的原始数组一般情况下是不满足堆的条件，既然我们要可用大根段的性质进行排序，第一步当然是对原始数组进行处理，构建大根堆。

      2.根节点数据处理以及大根堆重构。构建了大根堆之后，根节点的数据是最大值，将该数值取出，对剩下的元素重构大根堆，这时根节点是剩下元素的最大值，取出。只要不断重复上述的操作，不断取出未排序元素的最大值，直到未排序的元素只剩一个，就完成了排序工作。

 详见 http://www.cnblogs.com/yonghao/p/5140395.html

java代码见 https://blog.csdn.net/kimylrong/article/details/17150475

时间复杂度：nlogn，不稳定

冒泡排序

 对相邻的元素进行两两比较，顺序相反则进行交换，这样，每一趟会将最小或最大的元素“浮”到顶端，最终达到完全有序

/*
 * 冒泡排序
 */
public class BubbleSort {
　　public static void main(String[] args) {
　　　　int[] arr={6,3,8,2,9,1};
　　　　System.out.println("排序前数组为：");
　　　　for(int num:arr){
　　　　　　System.out.print(num+" ");
　　　　}
　　　　for(int i=0;i<arr.length-1;i++){//外层循环控制排序趟数
　　　　　　for(int j=0;j<arr.length-1-i;j++){//内层循环控制每一趟排序多少次
　　　　　　　　if(arr[j]>arr[j+1]){
　　　　　　　　　　int temp=arr[j];
　　　　　　　　　　arr[j]=arr[j+1];
　　　　　　　　　　arr[j+1]=temp;
　　　　　　　　}
　　　　　　}
　　　　} 
　　　　System.out.println();
　　　　System.out.println("排序后的数组为：");
 　　　　for(int num:arr){
 　　　　　　System.out.print(num+" ");
 　　　　} 
　　}
 }

如果我们的数据正序，只需要走一趟即可完成排序。所需的比较次数C和记录移动次数M均达到最小值，即：C_min=n-1;M_min=0;所以，冒泡排序最好的时间复杂度为O(n)

如果很不幸我们的数据是反序的，则需要进行n-1趟排序。每趟排序要进行n-i次比较(1≤i≤n-1)，所以，最坏的时间复杂度是O(n^2)

平均时间复杂度为O(n^2)

稳定

快速排序

1、先从数列中取出一个数作为基准数

2、分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边

3、再对左右区间重复第二步，直到各区间只有一个数

 

图解详见https://blog.csdn.net/it_zjyang/article/details/53406764

/**
 * 快速排序
 * @author IT_ZJYANG
 */
public class QuickSort {
    
    /**
     * 将数组的某一段元素进行划分，小的在左边，大的在右边
     * @param a
     * @param start
     * @param end
     * @return
     */
    public static int divide(int[] a, int start, int end){
        //每次都以最右边的元素作为基准值
        int base = a[end];
        //start一旦等于end，就说明左右两个指针合并到了同一位置，可以结束此轮循环。
        while(start < end){
            while(start < end && a[start] <= base)
                //从左边开始遍历，如果比基准值小，就继续向右走
                start++;
            //上面的while循环结束时，就说明当前的a[start]的值比基准值大，应与基准值进行交换
            if(start < end){
                //交换
                int temp = a[start];
                a[start] = a[end];
                a[end] = temp;
                //交换后，此时的那个被调换的值也同时调到了正确的位置(基准值右边)，因此右边也要同时向前移动一位
                end--;
            }    
            while(start < end && a[end] >= base)
                //从右边开始遍历，如果比基准值大，就继续向左走
                end--;
            //上面的while循环结束时，就说明当前的a[end]的值比基准值小，应与基准值进行交换
            if(start < end){
                //交换
                int temp = a[start];
                a[start] = a[end];
                a[end] = temp;
                //交换后，此时的那个被调换的值也同时调到了正确的位置(基准值左边)，因此左边也要同时向后移动一位
                start++;
            }    
            
        }
        //这里返回start或者end皆可，此时的start和end都为基准值所在的位置
        return end;
    }

    /**
     * 排序
     * @param a
     * @param start
     * @param end
     */
    public static void sort(int[] a, int start, int end){
        if(start > end){
            //如果只有一个元素，就不用再排下去了
            return;
        } 
        else{
            //如果不止一个元素，继续划分两边递归排序下去
            int partition = divide(a, start, end);
            sort(a, start, partition-1);
            sort(a, partition+1, end);
        }
            
    }
    
}

快速排序最“快”的地方在于左右两边能够快速同时递归排序下去，所以最优的情况是基准值刚好取在无序区的中间，这样能够最大效率地让两边排序，同时最大地减少递归划分的次数。此时的时间复杂度仅为O(NlogN)。
快速排序也有存在不足的情况，当每次划分基准值时，得到的基准值总是当前无序区域里最大或最小的那个元素，这种情况下基准值的一边为空，另一边则依然存在着很多元素(仅仅比排序前少了一个)，此时时间复杂度为O(N*N)。

 平均时间复杂度O(NlogN)，空间复杂度(N)，不稳定

归并排序

归并排序分为两个过程：一是数组划分为两个子数组并分别进行排序，二是将两个已排序的子数组进行合并

详见http://www.cnblogs.com/yonghao/p/5143364.html

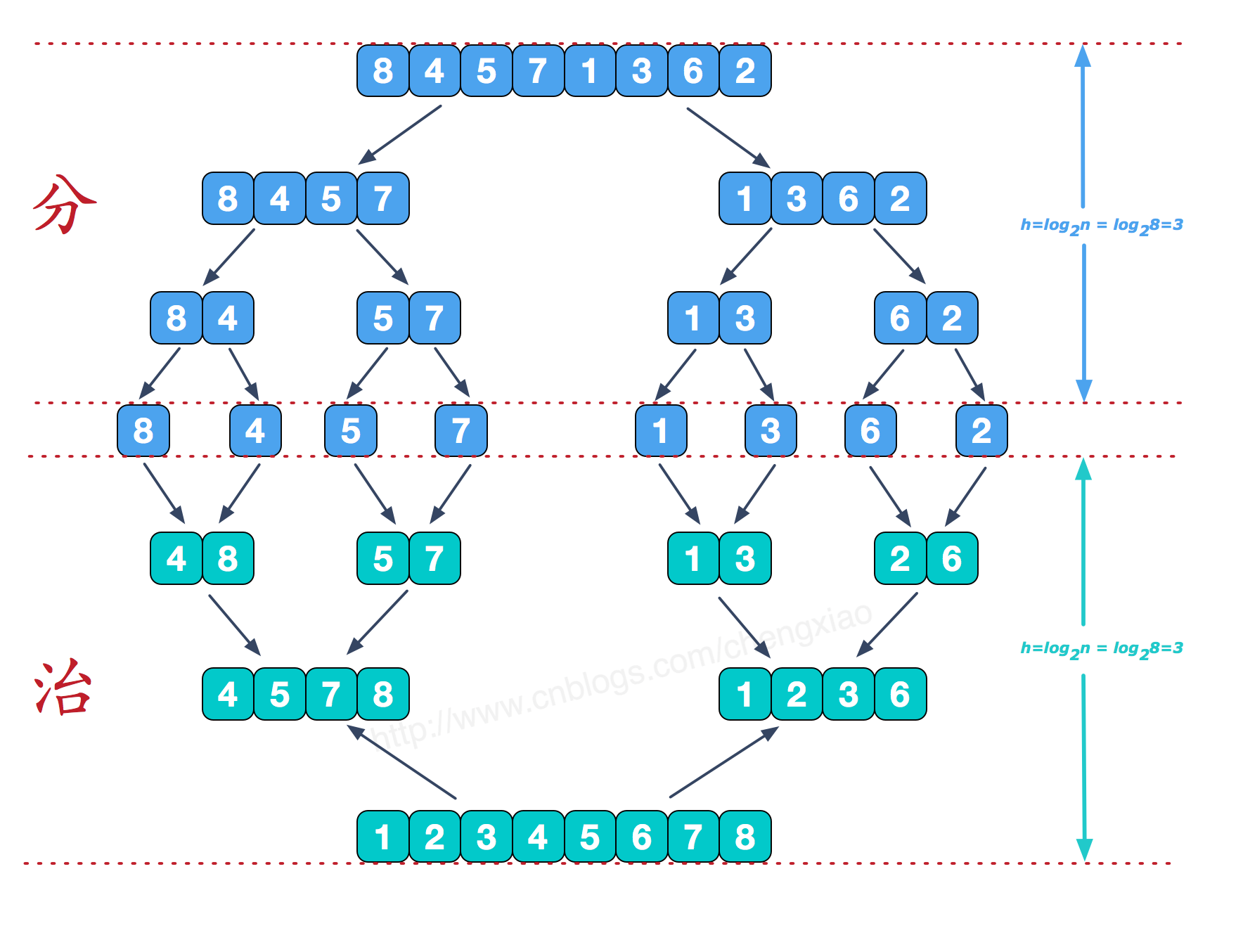
代码详见https://www.cnblogs.com/chengxiao/p/6194356.html

基数排序

 首先根据个位数的数值，在走访数值时将它们分配至编号0到9的桶子中

接下来将这些桶子中的数值重新串接起来，接着再进行一次分配，这次是根据十位数来分配

 基数排序是一个快速的稳定排序算法。其时间复杂度可以表示为O(Kn)。其中n就是待排序序列的元素个数，K是数字的位数

 java代码见https://www.cnblogs.com/dwj411024/p/5978821.html

各类排序算法的比较

详见http://blog.csdn.net/sysukehan/article/details/52661295