Graph representation learning

图表示学习的本质

找一个mapping函数（将原始空间中的点映射到嵌入空间中）同时可以使原始空间中所有点（高维向量）间的相似度（相对距离关系）在嵌入空间中得以保持。

---

怎么定义两个向量的距离？？

在二维空间中，一般用欧几里得距离即L2范数表示相似度（就是距离）；但是高维空间中，一般用余弦距离衡量空间距离。

两个向量的点积 = |A|* |B| *cos<A, B>，可见，单位向量的点积就是余弦相似度！

余弦距离dist = 1- cos<A, B> ，【0，2】

从公式看空间中向量最远的距离就是两向量反向，最近就是同向。向量直角，则余弦距离为1。
从原始空间到嵌入空间，我们用一个相同的函数来衡量空间中的关系，在原始空间我用一个f = 1-cos<A,B> 来衡量，到了嵌入空间还是希望满足这个函数。

当然，选择了余弦距离：一定程度上我们更重视向量的方向，忽视向量的幅值。

即在高维空间中比较相似度前提必须归一化！！！ 这样才能用相似度衡量距离。

显然，在同一维度空间（等长）中，两个单位向量，cos值 = 1 时是重合的，此时theta = 0,dist = 0， 即两个向量在高维空间中所表示的两个点是完全重合的。

本质上：是用向量的余弦值来衡量两个向量(高维空间中的点)间的位置。

为什么向量点积就是余弦相似度？？？

这里的前提是两个同维度空间中的单位向量，在同维度向量空间中单位化后的向量，比较是否相似其实就是比较方向（向量夹角），两向量夹角为0即重合时，显然最相似（完全一致嘛）。所以我们需要找一个函数来衡量向量夹角，向量间夹角的cos值很容易通过点积得到，因此cos值（余弦相似度）很适合作为这个衡量函数。显然，点积（余弦相似度）越大时, 俩单位向量夹角越小，越相似（余弦距离1-cos越小）。

以余弦距离作为距离衡量的优点：
可以忽略向量本身的模长，仅考虑张成的两个向量的夹角，与向量的幅值（模长）无关。
比如两篇文本向量化之后，就可以忽略掉由于文本长度不同导致的问题。
即余弦距离仅考虑两个向量指向是否相同，不考虑大小！但是实用性如何？？

直观的解释是：如果 x 高的地方 y 也比较高， x 低的地方 y 也比较低，那么整体的内积是偏大的，也就是说 x 和 y 是相似的。举个例子，在一段长的序列信号 A 中寻找哪一段与短序列信号 a 最匹配，只需要将 a 从 A 信号开头逐个向后平移，每次平移做一次内积，内积最大的相似度最大。

嵌入方式

1. 随机漫步嵌入：
   即我们将余弦相似度用来衡量从一个节点随机漫步时会访问到另一个节点的概率估计
   （本质上我们认为，一个节点随机漫步访问到离他距离最近的节点的可能性更大）、

Random walk co-occurences:从一节点V出发，会访问节点U的概率
这个概率也选用余弦相似度衡量

为何很多地方要用log函数作为损失优化？
Log首先是可以压缩范围，其次最重要的log可以将乘积的优化变成sum求和的优化。

节点u是节点V的邻居节点：就是指从节点V出发，漫步N次后能访问到U节点（访问过！）

损失函数就是想：给出一个节点V，预测节点U恰好是它的邻居的概率。

我们优化的就是：对于原空间所有点V的对应的自身邻居节点的集合N，对应到嵌入空间中
每两个点之间Z，在嵌入空间，“同时发生着V中每个节点u对于其所有邻居节点v，随机漫步N步后，访问过嵌入空间的v的概率最大（比上访问所有点--而不是邻居点相似度之和的概率）。

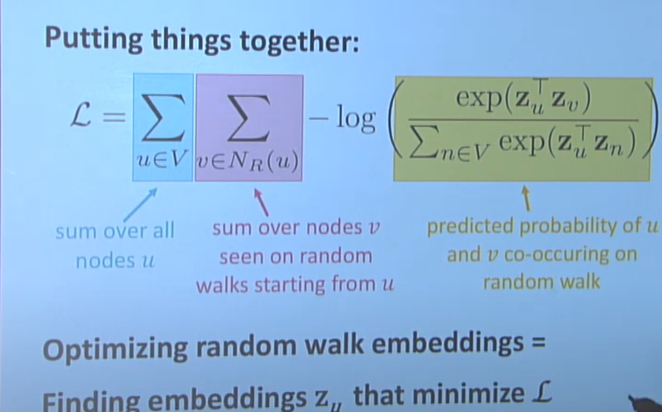
如果不是有log,应该是一个很长的连乘，长度是原始空间中的节点数n1*每个节点的邻居节点数n2,即将每个节点所有的邻居节点数目都乘到一起。

为什么要用漫步策略来确定邻居集合？
因为首先要确定连通性。在联通性确定的邻居节点去满足余弦相似度。

什么样的漫步策略：定长步数，随机无偏的从起始点漫步。

漫步可以分为两种策略：

1. 深度优先： deep-first search 每步都先走完起始节点的1度节点，再去走起始节点的2度节点（固定步数下 local 信息好，认为广度优先遍历具有整体的宏观视野）
2. 广度优先: breadth-first search：尽可能用最少的步数深入到最高度节点。（固定步数下走的距离最远，认为深度优先遍历具有局部的微观视觉）

因此根据随机漫步生成邻居节点集合就有两个超参数：

1. p返回参数，即从当前节点退回到小1度的邻居节点（定义此处概率为1/p)
2. q继续向深度走的参数，即从当前节点走到大1度的邻居节点（定义此处概率为1/q)
3. 向同度的邻居节点漫步的概率是1

即通过设置p和q的大小，可以控制整体的漫步策略是返回出发点还是走向更远点。

因此设置漫步策略时有两种情况：

1. p小一些，倾向于广度优先搜索（走到当前步之后会有更大几率回到前一步，此时的前一步是小1度距离的所有节点，而不是只是来时的那个小1度节点，因此倾向于广度）
2. q小一些，倾向于深度优先搜索

如何衡量嵌入后的结果的稳定性：

随机去掉或增加一定比例数目的连接线，看对基于嵌入节点属性的预测任务的准确性
实验表明，基于以上的随机漫步优化得到的嵌入空间节点对于以上扰动都具有很强的稳定性。

针对嵌入空间的节点，可以做很多通常的任务：

1. 节点分类，送入分类器即可
2. 聚类
3. 连接预测:根据两个节点的属性去预测边的权重（可以拼接后做激活得到结果，也可以哈德马积再激活，还可以直接求和或者求平局或者求L2范数再激活作为边权）

我们要做的最原始的东西是要在嵌入空间也能反应原空间的相似性：但是我们有多种定义相似性的方法：如

1. 随机漫步相似定义（上述）
2. 邻接矩阵相似定义
3. Node2vec相似定义
4. Multi-hop相似度定义

没有一个相似定义能在所有场景做到最好：因此首先应根据应用场景选择相似定义。据文章知：

1. node2vec更适合分类场景
2. Multi-hop更适合连接预测
3. 随机漫步计算更经济

以上都是针对单个节点的嵌入，最终将原空间的节点嵌入到嵌入空间还是相同的节点数量，那么如何嵌入整张graph到嵌入空间中得到一个嵌入节点呢？？
比如以下graph任务：

1. 预测一个复杂分子是否有毒
2. 识别异常的图

方法1：直接做常规的graph嵌入，节点数目不变；然后对所有节点做加和或平均得到一个节点。。
方法2：在原空间取部分节点做一定策略如平均等先得到一个虚拟点，再将此虚拟点嵌入到embedding space
方法3：匿名漫步嵌入