打了一场cf模拟赛,zbl
发现宝藏,建议去看看awa https://www.bilibili.com/video/BV1Cg4y1871L
T1Filling Diamonds
cout<<read()<<endl;
简单题,随便推一推就好了
T2 Sorted Adjacent Differences
我只想说wtnl
吐了。。。
我看t<=10^4,n<=10^5
以为要O(n)才能过。。。
直接就把排序给排除了。。。
正解是构造,要排序。。。
这就是道简单题,我硬是用了1个半小时+去写。。。
我真是服了我自己了。淦!
T3 我没有仔细看,时间不够了。。。
好像是个大水题啊淦
血亏。。。
因为懒得订正(逃)就没有继续写题解了awa,反正是大水题
T4Edge Weight Assignment
#define 奇数边 奇数长的边
#define 偶数边 偶数长的边
好水啊啊啊啊啊啊
我裂了,调了1个多小时
这题其实不难
对于题目要求的两个东西,可以很容易的发现他们并没有任何关系
所以这需要分开来求
最小的话并不难求
异或的一个基本的性质大家应该都知道:a^a=0,就是任何一个数异或它本身都是0
那么为了最小,我们可以发现之间是偶数边的叶子节点都是用一个数就可以得到最小值0
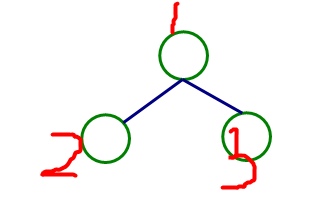
像这个图,我们很明显可以使(1,3)与(1,2)相等,这样的话异或和就是0
偶数都可以像这样做
接下来就考虑奇数边
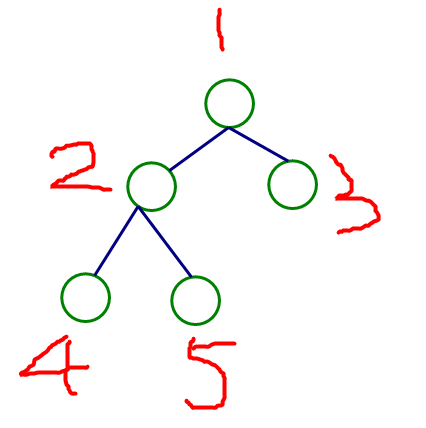
如这个图,4与3之间是奇数边
我们可以发现,3条边的话,也是可以使异或和为0的,如5,10,15等等,都可以
那么任何两个叶子节点之间,必然是有两个及以上的边相连的。
现在我们可以说是的得到了基数2和3,可以发现,任何数量的边都可以由此计算出来。
所以答案只有1或3.
那这就很妙了啊awa
我们就只用判断是否有奇数边就好了
这个只用染色一下就可以O(1)判断了
妙啊awa
最短解决
那么对于最长呢?
更简单
可以发现,对于任何长于2的边都可以用不同的数异或来产生0
但是如果是这样的呢
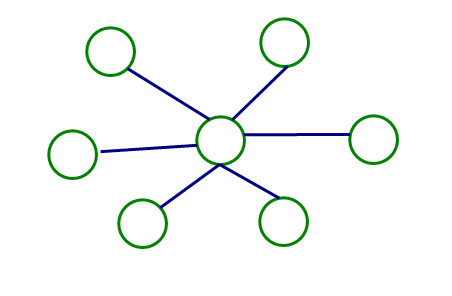
这样的话只能用一个数了。
所以需要判断是不是多个叶节点同时连接在一个节点上,如果是就要减掉。
然后就解决了awa
妙啊~~~awa
附上代码
#include<bits/stdc++.h> #define ll long long using namespace std; struct edge { int next,to; }e[200001]; int head[200001],n,m,tot,ru[100001],color[100001],root,leave[100001],ans;bool vis[100001]; inline ll read() { char c=getchar();int a=1,b=0; for(;c<'0'||c>'9';c=getchar())if(c=='-')a=-1; for(;c>='0'&&c<='9';c=getchar())b=b*10+c-48; return a*b; } void add(int i,int j) { leave[i]++;leave[j]++; e[++tot].next=head[i]; e[tot].to=j; head[i]=tot; ru[i]++; swap(i,j); e[++tot].next=head[i]; e[tot].to=j; head[i]=tot; ru[i]++; } void bfs() { queue<pair<int,int> > q; q.push(make_pair(root,1)); while(q.size()!=0) { pair<int,int> x=q.front(); q.pop(); int xx=x.first; bool flag=false; if(x.second==1) { color[xx]=2; flag=false; } else { color[xx]=1; flag=true; } for(int i=head[xx];i!=0;i=e[i].next) { int u=e[i].to; if(color[u]!=0)continue; if(flag==true) { q.push(make_pair(u,1)); } else if(flag==false) { q.push(make_pair(u,2)); } } } } bool dfs(int x,int fa) { int flag=false,sum=0; for(int i=head[x];i!=0;i=e[i].next) { int u=e[i].to; if(u==fa)continue; flag=true; int aa=dfs(u,x); if(aa==true) { sum++; } } if(flag==false) { return true; } if(sum>1) { ans-=(sum-1); } return false; } int main() { n=read(); for(int i=1;i<n;i++) { add(read(),read()); } for(int i=1;i<=n;i++) { if(ru[i]>=2) { root=i; break; } } bfs(); for(int i=1;i<=n;i++) { if(leave[i]!=1) { leave[i]=0; } } int flag=false;bool cot=false; for(int i=1;i<=n;i++) { if(leave[i]==true&&color[i]!=1) { if(flag==1) { cout<<3<<endl; cot=true; break; } if(flag==0) { flag=2; } } if(leave[i]==true&&color[i]!=2) { if(flag==2) { cout<<3<<' '; cot=true; break; } if(flag==0) { flag=1; } } } if(cot==false) cout<<1<<' '; ans=n-1; dfs(root,0); cout<<ans<<endl; return 0; }
emmmm
T5莫得时间了awa
不写了
总结:
T1,T2和T3应该是秒掉的,对于这样的题目不应该消耗太多时间在里面。这一次get到了一个应该有的技能,染色判断边长奇偶性。这确实 很 妙 awa
还有就是,像T2这样的题目,数据范围无法支持O(n^2)的,应该绝大多数是构造,枚举是不行的。
这应该是一个套路了。
当然,其实O(n^2)的话这个应该也会是和图论结合,建图去跑最小生成树。是可以做的。
awa
学了这么久,我还是这么菜啊awa
zbl