卡特兰数是一种经典的组合数,经常出现在各种计算中,其前几项为 : 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190 ...
它最基本的递推为
f(n)=f(0)*f(n-1) + f(1)*f(n-2) + ... + f(n-1)*f(0) (n>=2, f(1)=1, f(0)=1)
应用
一.比如说要求由n个节点组成的二叉树个数,可以这样思考:
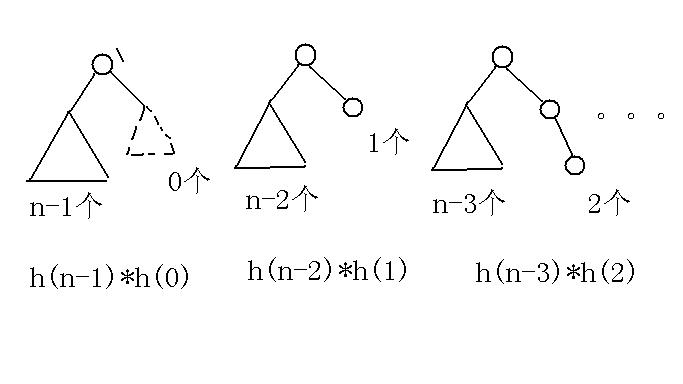
所以很容易发现符合卡特兰数的递推式啦。
二.给定n个数字1,2,3,4...,n,求它们出栈顺序的方案数。
(这次就不画图了。。
设出栈的最后一个元素为k,那么入栈k之前的k-1个元素出栈方案数为h(k-1),k入栈后,k之后的n-k个元素出栈方案为h(n-k),则k最后出栈的方案数为,h(k-1)*h(n-k),不同k之间的方案数显然没有联系,所以之间是加法关系,加起来就好了。明显可以看出是卡特兰数。
三.给一个n条边的凸多变形,用几条不相交的顶点连线,把它分成若干三角形,求有几种划分方案
 (图画的好丑,不要介意)
(图画的好丑,不要介意)
考虑把这个八边形划分成1,2两个部分,那么多边形1就是六边形,多边形2是4边形。所以这种划分方式的总方案为h(6-3)*h(4-3),不同的划分方案的值加起来,就是卡特兰数了。