今天农历28,哈哈明天就能放假过年啦~
都快省选了,才发现自己已经很久没有做过计算几何的题目了,然后匆匆忙忙跑去做了一题很简单的
1069: [SCOI2007]最大土地面积
然后这篇博文就作为一个大杂烩,把这几天做过的计算几何的知识点都丢到里面好了(反正给是给自己看
极角排序
我习惯用叉积进行排序。
cmp函数里,先按象限来排,同象限的用叉积比较谁在谁的逆时针方向,如果在同一条直线上,比较横坐标。
 向量的运算什么的用重载运算符什么的比较方便吧。
向量的运算什么的用重载运算符什么的比较方便吧。
1 int Xx(P a){ 2 if(a.x-O.x>0 &&a.y-O.y>=0)return 1; 3 if(a.x-O.x<=0&&a.y-O.y>0 )return 2; 4 if(a.x-O.x<0 &&a.y-O.y<=0)return 3; 5 if(a.x-O.x>=0&&a.y-O.y<0 )return 4; 6 } 7 bool cmp(const P a,const P b){ 8 int aX=Xx(a); 9 int bX=Xx(b); 10 if(aX!=bX)return aX<bX; 11 double cx= (a-O)*(b-O); 12 if(cx==0)return a.x<b.x; 13 else return cx>0; 14 }
凸包
凸包也比较基础吧,用一个栈来维护,每次叉积来判逆时针,顺时针,按排好的极角顺序就可以了。
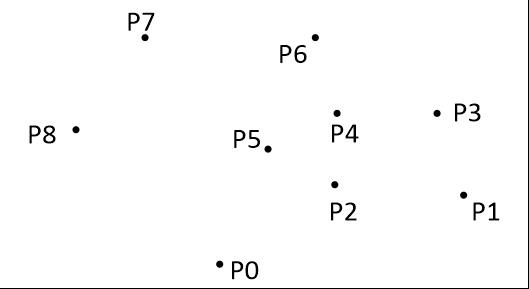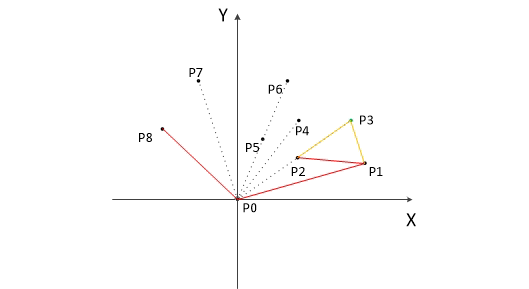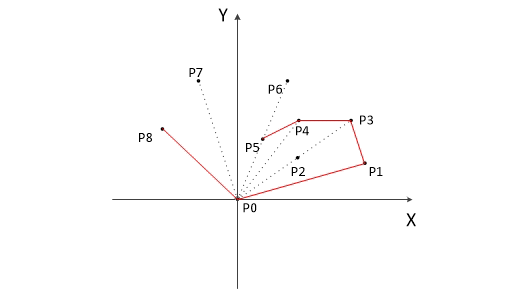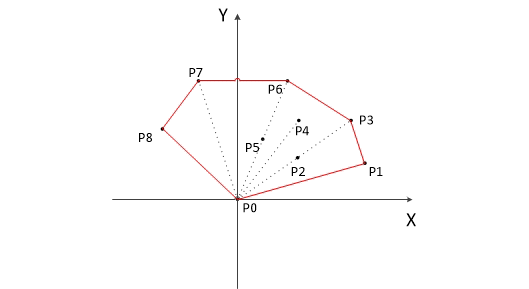
叉积为正->逆时针
叉积为负->顺时针
1 void TuBao(){ 2 st[++top]=p[1]; 3 st[++top]=p[2]; 4 For(i,3,n+1){ 5 while( (p[i]-st[top-1])*(st[top]-st[top-1])>=0 ) top--; 6 st[++top]=p[i]; 7 } 8 }
旋转卡(qia)壳
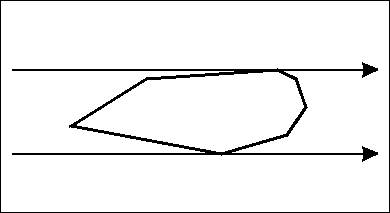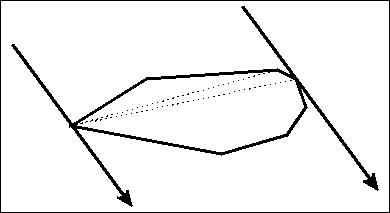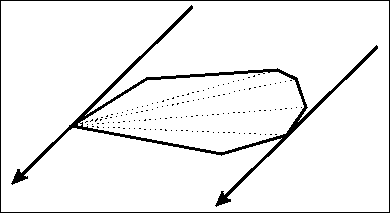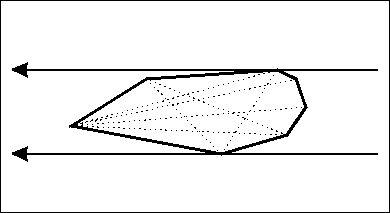
想象两条平行线绕着一个凸多变形转啊转
具体实现方法其实是在找最大三角形的过程
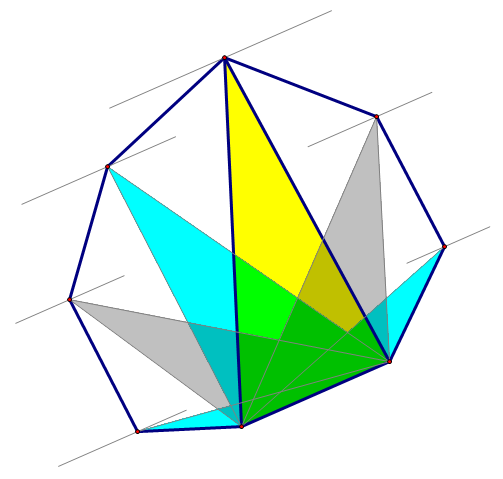
核心代码:
1 Ni=(i1+1)%top; 2 Np=st[Ni]; 3 while(Ni!=x&&(Np-st[y])*(st[x]-st[y])>(p1-st[y])*(st[x]-st[y])){ 4 i1=Ni; p1=Np; 5 Ni=(i1+1)%top; Np=st[Ni]; 6 }
线段相交
只要会线段相交,其实直线相交也一样(把线段的长度设长一点就可以了)
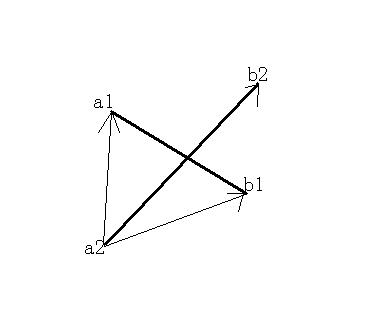
以其中的 a2b2 为中间向量必须保证a1与b1在a2b2的两边,叉积判断。也要用a1b1为中间向量判断一次,避免如下情况。
代码~
1 bool XX(ED L1,ED L2){ 2 P a1,a2,b1,b2; 3 a1=L1.a; a2=L2.a; 4 b1=L1.b; b2=L2.b; 5 double cx1,cx2; 6 int t1=0,t2=0; 7 8 cx1= (a2-a1)*(b1-a1); 9 cx2= (b2-a1)*(b1-a1); 10 if(cx1*cx2<0)t1=1; 11 12 cx1= (a1-a2)*(b2-a2); 13 cx2= (b1-a2)*(b2-a2); 14 if(cx1*cx2<0)t2=1; 15 16 if(t1&&t2)return 1; 17 else return 0; 18 }
两直线交点(向量法)
采用向量法就不需要担心斜率不存在之类的问题了(还要特判确实比较麻烦)
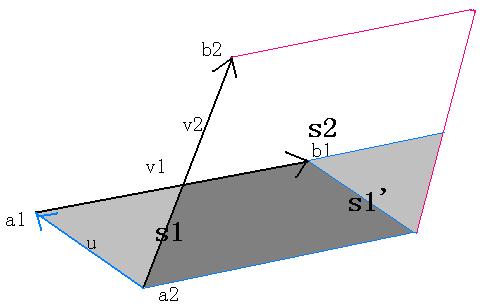
s1与s1'两块平行四边形的面积是一样的。
设交点为P
设 t= |Pa2|/|b2P| ,求出t后就可以通过向量加减得到P的坐标了。
而 t=S2/S1',又S1'==S1(等底同高),所以t=S2-S1;
S1与S2可以分别通过 u与v1 v2与v1叉乘而得,就与P点坐标无关了。
1 P X(L l1,L l2){ 2 P v1,v2,u; 3 v1=l1.b-l1.a; v2=l2.b-l2.a; 4 u=l1.a-l2.a; 5 double t=(u*v2)/(v2*v1); ; 6 P as; 7 as=l1.a+v1*t; 8 return as; 9 }
半平面交
其实不会很难,学的时候看了很多个博客,本来想抄个模板,最后还是靠自己写出来了(自己写的程序才是真正的板子)
和数学里的线性规划其实是差不多的。
用双头队列维护,每次在两边减去范围外的边,最后就能把多边形的核求出来了。

一开始极角排序的时候要注意把平行的直线排好,等一下去重方便。
用象限加叉积的方法极角排精度更高比较不容易出错。
1 void HPI(){ 2 int L=1,R=2; 3 q[L]=l[1]; q[R]=l[2]; 4 For(i,3,m){ 5 while(L<R&&Right(X(q[R],q[R-1]),l[i]))R--; 6 while(L<R&&Right(X(q[L],q[L+1]),l[i]))L++; 7 q[++R]=l[i]; 8 } 9 while(L<R&&Right(X(q[R],q[R-1]),q[L]))R--; 10 if(R-L<=1){ 11 printf("0.000"); 12 return; 13 } 14 q[L-1]=q[R]; 15 int tt=0; 16 For(i,L,R) p[++tt]=X(q[i],q[i-1]); 17 db fn=0; 18 For(i,3,tt){ 19 fn+=(p[i-1]-p[1])*(p[i]-p[1])*0.5; 20 } 21 printf("%.03lf ",fn); 22 }
本题写的是求核的面积 X()函数就是上面写的求交点的函数。