题意
给定(n)个点的带边权树,(m)条代价路径,令两条路径((u_1,v_1,w_1)(u_)(u_2,v_2,w_2)),(val=sumlimits_{(u,v)in dis(u_1,v_1)~or~(u,v)in dis(u_2,v_2)}val(u,v)-w_1-w_2)。求(max_{i,j,i eq j}{val_{i,j}})。
做法
令(x)到根的边权和为(len_x)
lca不同
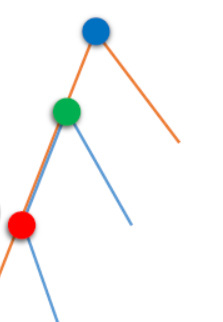
令黄色链,长度为(len_1),代价为(val_1),lca为(lca_1)。蓝色:(len_2,val_2,lca_2)
令红色点为(x)
(val=len_1+len_2-len(x)+max(len(lca_1),len(lca_2))-val_1-val_2)
考虑对每个点(x),线段树维护
(f_i):路径一端在(x)子树,链的lca的深度为(i),链长度-代价的最大值
(g_i):路径一端在(x)子树,链的lca的深度为(i),链长度-代价+(len_{lca})的最大值
可以线段树合并维护。值得注意的细节是,处理完x的子树后,将([dep_x-1,n])清空
答案的更新可以通过:(fa_x=y),将(y)合并给(x)时左子树右子树这样更新一下
lca相同
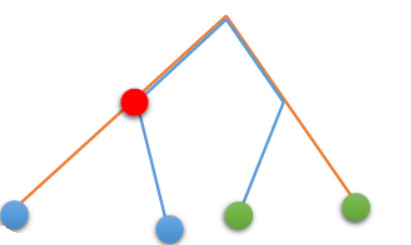
枚举lca,建虚树
(val=)(路径长度和+蓝点间路径+绿点路径)/2-代价
枚举蓝点的lca,令蓝点为(a,b),对应的绿点分别为(p_a,p_b)
相当于最大化:(dis(p_a,p_b)+dis(a,p_a)+dis(b,p_b)-2cost(a,p_a)-2cost(b,p_b)+len(a)+len(b)-2len(lca))
发现除去(dis(p_a,p_b)),其他的都是独立的
由于枚举了(lca),则无需管(2len(lca))。对绿点下面新建一个叶子节点,其边权为上述需要维护的。
不过边权可能为负,不过由于是叶子节点,新加入点作为端点的最长路径另一端点必定为原直径端点依然成立