[算法模版]Tarjan爷爷的几种图论算法
前言
Tarjan爷爷发明了很多图论算法,这些图论算法有很多相似之处(其中一个就是我都不会)。这里会对这三种算法进行简单介绍。
定义
强连通(strongly connected): 在一个有向图(G)里,设两个点a, b 发现,由(a)有一条路可以走到(b),由(b)又有一条路可以走到(a),我们就叫这两个顶点(a,b)强连通。
强连通图: 如果 在一个有向图(G)中,每两个点都强连通,我们就叫这个图,强连通图。
分量:把一个向量分解成几个方向的向量的和,那些方向上的向量就叫做该向量(未分解前的向量)的分量。
强连通分量(strongly connected components/SCC):在一个有向图G中,有一个子图,这个子图每2个点都满足强连通,我们就叫这个子图叫做强连通分量。
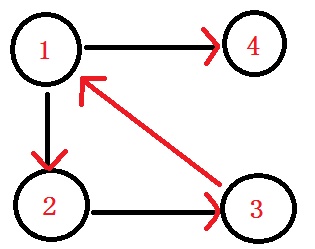
比如说这个图,在这个图中呢,点1与点2互相都有路径到达对方,所以它们强连通。
而在这个有向图中,点1 2 3组成的这个子图,是整个有向图中的强连通分量。
dfn[i]:指第(i)个点的(dfs)序。
low[i]:指第(i)个点的子树内的所有点通过反祖边能走到的点的(dfn)的最小值。
先行结论
- 在一个无向图上,跑一棵生成树。可以证明非树边只有反祖边,没有横叉边。
Tarjan算法求割点/割边(针对无向图)
割点
首先,一个比较显然的结论就是所有的叶子结点和根节点都不是割点。对于其他节点u来说,只要有至少一个儿子v满足low[u]>=dfn[v],就证明v若不通过他父亲就回不去。那这个点就是割点。根节点只需要判断是不是有两棵子树就好了。实现起来可以当作有两个点满足low[u]>=dfn[b]。因为因为根节点(dfn)为1,所以一定满足条件。如果两个根结点儿子不通过根节点就能联通,那么他们一定在一个子树。
void tarjan(int now,int ff){
low[now]=dfn[now]=++idx;
for(int i=head[now];i;i=side[i].next){
int v=side[i].v;
if(side[i].id==ff)continue;
if(!dfn[v]){
tarjan(v,side[i].id);
low[now]=min(low[now],low[v]);
if(low[v]>=dfn[now]){ans[now]++;}
}
else{
low[now]=min(dfn[v],low[now]);
}
}
return;
}
void output(){
for(int i=1;i<=n;i++){
if((ans[i]&&!root[i])||(ans[i]>=2&&root[i])){
cout<<i<<' ';//输出所有割点
}
}
}
割边
和割点基本一样。只需要把(low[v]>=dfn[u])改成(low[v]>dfn[u])即可。同时需要判断,不能再次走刚刚走过的边。
如果点u的至少一个儿子v满足low[v]>dfn[u]。就证明不通过这条边无法走到上面。所以这是条割边。
Tarjan算法求点双/边双(针对无向图)
边双
和楼下的强连通分量很像,唯一的区别就是需要特殊判断一下,不能通过从父亲下来的那条边走上去。(因为强连通分量是有向图,走不上去,所以不存在这个问题)
实现起来也很简单,只用简单修改一下dfs函数:
dfs(u,f)其中u为当前节点,f为走到这个点通过的边的编号。
当在遍历u的所有边试图向下dfs时,只需要加一个if(现在准备选择的边的编号==f)continue;即可。
点双
咕咕咕
Tarjan算法求强连通分量(针对有向图)
stack<int> tp;
void dfs(int u)
{
dfn[u]=low[u]=++cnt1;//初始化每个未访问过的节点
tp.push(u);
for(int i=head[u];i;i=side[i].next)
{
int v=side[i].v;
if(!dfn[v])dfs(v),low[u]=min(low[u],low[v]);
else if(!scc[v])low[u]=min(low[u],dfn[v]);//被访问过却没有SCC编号(在栈里),证明在同一个强连通分量。因为栈维护的是一条有一个节点到它儿子的路径。所以如果栈顶的点u到栈中任意一点v有边。就证明存在u到v的一个环。
}
if(dfn[u]==low[u])//如果这个点是它所在强连通分量中dfn最小的,则有它来承担输出整个SCC的任务
{
int s=tp.top(),id=++cnt2;tp.pop();
scc[s]=id;
while(s!=u)s=tp.top(),tp.pop(),scc[s]=id;
}
}
参考资料
