状压dp 图论 难题 E. String Transformation 2
题目大意:
你有两个串, (A) 和 (B) ,你可以对A进行操作使得 (A=B)
操作:选择k个相同的字符,然后把他们修改成相同的字符。
题目保证 (A) (B) 只有字母表的前二十个字符。
题解:
这个题目确实很难,不过刘雨小姐姐也是真的强,把这个题目转化成求最大的有向无环图。
这个题目的题解答案就是 :(2*n-S-1) 这个(S) 就是最大有向无环图的点的数量。
至于为什么是这个答案呢?
假设 (A) 变成 (B) 是一个有向无环图,那么就是说和版本1是一样的。
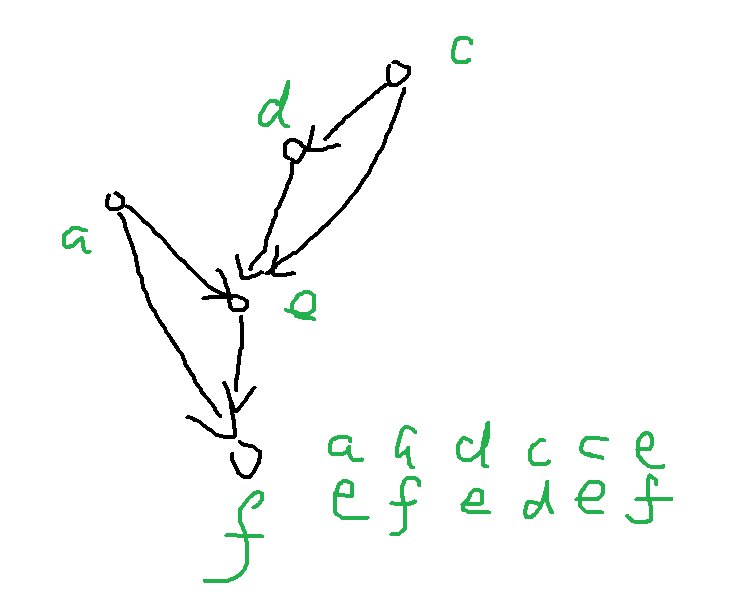
那么对这个图标一个优先级,让优先级低的往优先级高的跳。
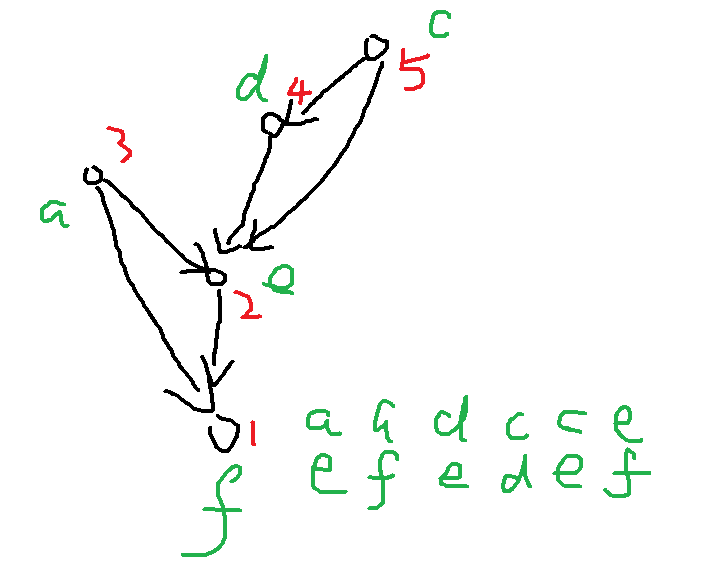
注意这个点的3和4的优先级无所谓,但是标4为3,那么5一定是4。
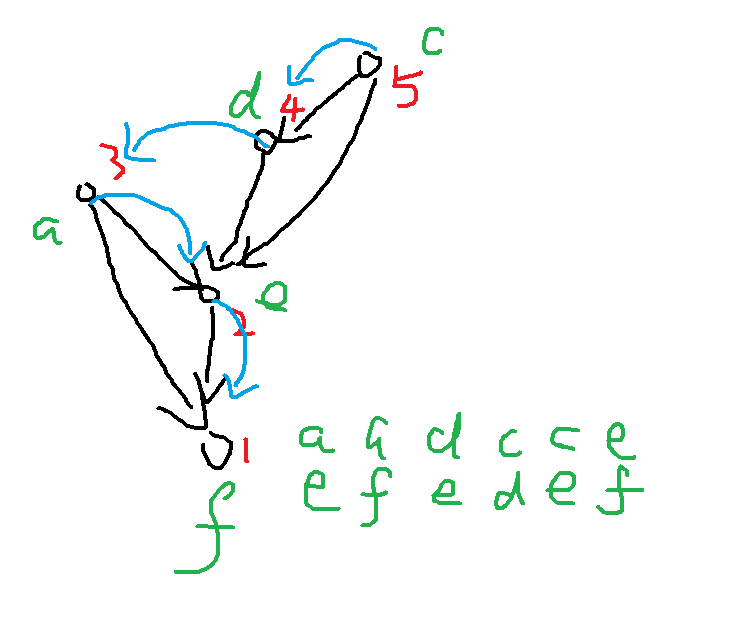
很容易发现答案就是这个有向无环图的点的数量-1,就是要跳的次数,因为版本1规定了跳的方向,一定是往字符大的方向跳,所以不会形成环,就是一个有向无环图,那么如果加入了一个点,使得这个图出现环了呢?
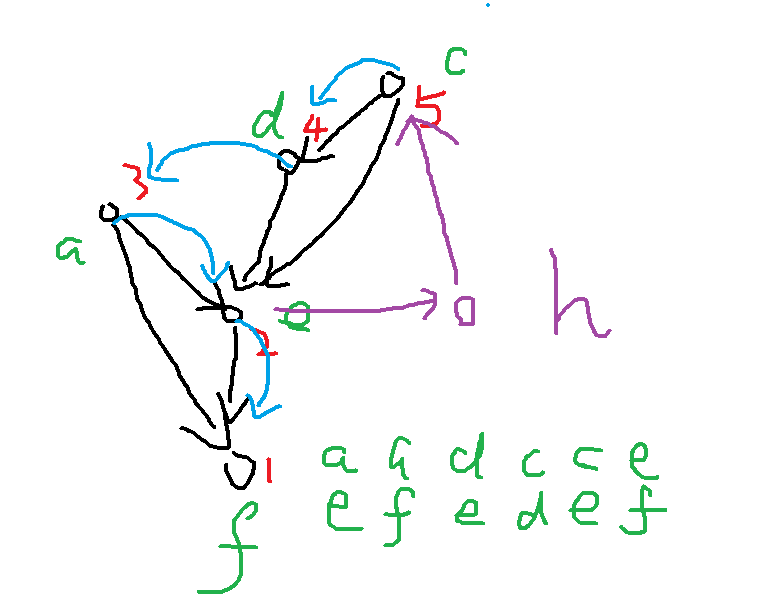
这样的话,是不是最多就要多跳两次。
因为这个点一定要跳出去,所以一次,别人一定要跳到它,所以一次,至少也要两次,所以加入的这个点如果构成环了,那么会多跳两次。
本来是每一个点的贡献都是2,但是形成有向无环图之后它只要跳出去一次就一定可以到达终点,所以会减少一次,对于终点1,就只要0次,减少了两次。
所以最后答案就是 :(2*n-S-X) 其中 (S) 表示所有独立的最大有向无环图的点数相加,(X) 表示独立的有向无环图的数量。
最后怎么求最大的有向无环图呢,这个可以状压求。
首先预处理一下每一个点指向的位置,定义(dp[s]) 表示状态 (s) 下,是否为一个有向无环图,每一个点加入这个状态的要求它指向的点都不在状态 (s) 中,那么就可以加入。
判断图的数量可以用并查集。
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define inf64 0x3f3f3f3f3f3f3f3f
using namespace std;
const int maxn = 1e5+10;
char A[maxn],B[maxn];
int f[30],to[30];
int findx(int x){
return f[x]==x?x:f[x]=findx(f[x]);
}
void unite(int x,int y){
x = findx(x);
y = findx(y);
if(x==y) return ;
f[x]=y;
}
bool dp[1<<21];
int main(){
int t;
scanf("%d",&t);
while(t--){
int n;
scanf("%d",&n);
scanf("%s%s",A+1,B+1);
for(int i=0;i<20;i++) f[i]=i,to[i]=0;
for(int i=1;i<=n;i++){
int x = A[i]-'a', y = B[i]-'a';
to[x]|=(1<<y);
unite(x,y);
}
int ans = 40;
for(int i=0;i<20;i++) if(findx(i)==i) ans--;
memset(dp,false,sizeof(dp));
dp[0]=true;
int maxs = 0;
for(int s=0;s<(1<<20);s++){
if(!dp[s]) continue;
int cur = 0;
for(int i=0;i<20;i++){
int tmp = 1<<i;
if(tmp&s) cur++;
if(to[i]&s) continue;
dp[s|tmp]=true;
}
maxs=max(maxs,cur);
}
printf("%d
",ans-maxs);
}
return 0;
}
/*
2
4
cabc
abcb
*/