【凸优化】【长链剖分】【2019冬令营模拟1.8】tree

PROMBLEM

给你一棵树，你需要在树上选择恰好 m条点不相交的、长度至少为 k的路径，使得路径所覆盖的点权和尽可能大。求最大点权和。
数据保证有解。

SOLUTION

• 这是一道综合的题目，考察凸优化、长链剖分、树形DP、以及关于数组空间的优化

• 首先引进凸优化

  • 凸优化就是关于答案可以表示成一个凸函数 f(x)，x是题目给出的参数，并且 这个函数的斜率成下降的趋势（反过来也可以）
    
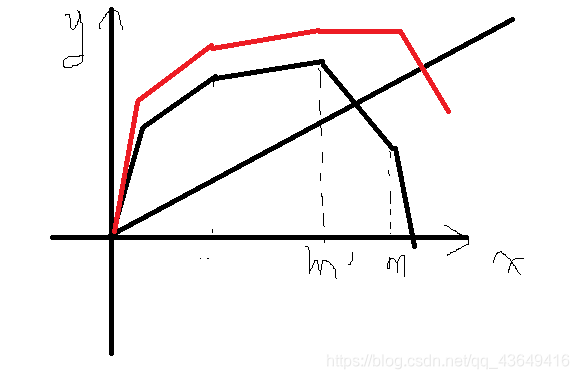
  • 假设我们已知的函数的最大值是f(m’)，而我们要求的是f(m)，发现m在m’的后面。
  • 我们这个时候可以给这个凸函数加上一个正比例函数，具体就是f '(x)=f (x)+kx
  • 那么我们会发现对应的x越大，加上的这个值就会越大，相对来说m就会比m’的增量更大，那么当这个k到一定范围时，我们的凸函数的最大值就会在m上，通过f '(x)就可以间接求出f(x)了。
  • 从图像上理解，就是将这个凸函数向上（逆时针方向）旋转。
  • 另外，如果这个最大值的m’在m的右边的话，我们就要将函数向下旋转，这样才能保证m能旋到最高处。
  • 对于下凸的函数可以类比解决。
  • 实现我们可以二分这个k，判断m’在m的哪边再旋转。

• 对于这题来说，我们可以感性地理解，选的链的个数越多我们每次的增量就越小，也就是斜率递减，那么就成了一个凸函数。那么我们就可以用这个性质把m给省去。于是就变成求最大值了。

• PS.所有的答案与点权都是整数，所以每次的增量也是整数，二分就不会存在精度问题。

• 我们显然可以运用树形DP，设f[x][i]表示以x为根的子树中，有一条以x为top的长度为i的链，符合题目的路径和这条链的总点权和。

  • 但是这个DP是N的三次方的。怎么优化它？
    1 枚举一个f[x][i]，发现可以与它合并的f[y][j]是一段连续的区间，可以用后缀max进行优化。变成N方复杂度
    2 运用长链剖分可以优化成O（n）
    • 长链剖分是什么？
    • 顾名思义，树链剖分是以子树大小做重儿子，长链剖分就是以子树的最大的深度的儿子作重儿子。因为所有的状态都以深度为关键字，我们只需要在每一条“轻边”的地方转移整一条“长链”，所有的结点只在一个长链里面，所以只会转移n次。
    • 这样做树形DP是O(n)的，空间复杂度还是N方的。但是一个点的重儿子遍历完之后它的信息被全部转移到这个点上，这个重儿子的空间就可以释放掉了。所以实际上可用空间还是O(n)的。
    • 实现上，我用的是DFS序去模拟f数组，也就是预留数组空间。

总时间复杂度O（nlog(S)），空间复杂度O(n)。
S表示点权绝对值之和。

附上代码（第一次打，非常非常丑 ）

#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#define maxn 150005
#define ll long long 
using namespace std;

int n,m,K,i,j,k,x,y,Mxk;
ll v[maxn],l,r,mid,Mx;
ll f[maxn],f0[maxn],g[maxn],g0[maxn],tag[maxn],tag0[maxn];
int em,e[maxn*2],nx[maxn*2],ls[maxn];
int dep[maxn],pson[maxn],mxdep[maxn],tot,dfn[maxn],fa[maxn];

void insert(int x,int y){
	em++; e[em]=y; nx[em]=ls[x]; ls[x]=em; 
	em++; e[em]=x; nx[em]=ls[y]; ls[y]=em;
}

void dfs(int x,int p){
	dep[x]=dep[p]+1; pson[x]=0; mxdep[x]=dep[x];
	for(int i=ls[x];i;i=nx[i]) if (e[i]!=p) {
		dfs(e[i],x);
		if (!pson[x]||mxdep[e[i]]>mxdep[x]) 
			mxdep[x]=mxdep[e[i]],pson[x]=e[i];
	}
}

void dfs2(int x,int p){
	dfn[x]=++tot; 
	if (pson[x]) fa[pson[x]]=fa[x],dfs2(pson[x],x);
	for(int i=ls[x];i;i=nx[i]) if (e[i]!=p&&e[i]!=pson[x])
		fa[e[i]]=e[i],dfs2(e[i],x);
}

void dfs3(int x,int p,ll D){
	ll s=0; int c=0; ll tmp; int tmpc;
	for(int i=ls[x];i;i=nx[i]) if (e[i]!=p)
		dfs3(e[i],x,D),s+=g[e[i]],c+=g0[e[i]];
	
	g[x]=s,g0[x]=c;
	tag[fa[x]]+=v[x]+s-g[pson[x]],tag0[fa[x]]+=c-g0[pson[x]];
	f[dfn[x]]=v[x]+s-tag[fa[x]];
	f0[dfn[x]]=c-tag0[fa[x]];
	if (mxdep[x]>dep[x]&&(f[dfn[x]+1]>f[dfn[x]]||
		f[dfn[x]+1]==f[dfn[x]]&&f0[dfn[x]+1]>f[dfn[x]])) 
			f[dfn[x]]=f[dfn[x]+1],f0[dfn[x]]=f0[dfn[x]+1];
			
	if (mxdep[x]-dep[x]+1>=K){
		tmp=f[dfn[x]+K-1]+tag[fa[x]]+D;
		tmpc=f0[dfn[x]+K-1]+tag0[fa[x]]+1;
		if (tmp>g[x]||tmp==g[x]&&tmpc>=g0[x]) 
			g[x]=tmp,g0[x]=tmpc;
	} 
	
	for(int i=ls[x];i;i=nx[i]) if (e[i]!=p&&e[i]!=pson[x]){
		int y=e[i];
		for(j=0;j<=mxdep[y]-dep[y];j++) if (K-j-1<=mxdep[x]-dep[x]+1) {
			tmp=-g[y]+f[dfn[y]+j]+tag[fa[y]]+f[dfn[x]+max(1,K-j-1)-1]+tag[fa[x]]+D;
			tmpc=-g0[y]+f0[dfn[y]+j]+f0[dfn[x]+max(1,K-j-1)-1]+tag0[fa[y]]+tag0[fa[x]]+1;
			if (tmp>g[x]||tmp==g[x]&&tmpc>g0[x]) g[x]=tmp,g0[x]=tmpc;
		}
		for(j=mxdep[y]-dep[y];j>=0;j--) {
			tmp=s-g[y]+f[dfn[y]+j]+tag[fa[y]]+v[x];
			tmpc=c-g0[y]+f0[dfn[y]+j]+tag0[fa[y]];
			if (tmp>f[dfn[x]+j+1]+tag[fa[x]]||
				tmp==f[dfn[x]+j+1]+tag[fa[x]]&&tmpc>f0[dfn[x]+j+1]+tag0[fa[x]]) 
					f[dfn[x]+j+1]=tmp-tag[fa[x]],f0[dfn[x]+j+1]=tmpc-tag0[fa[x]];
			if ((f[dfn[x]+j]<f[dfn[x]+j+1]||f[dfn[x]+j]==f[dfn[x]+j+1]&&f0[dfn[x]+j]<f0[dfn[x]+j+1]) 
			&&j+1<=mxdep[x]-dep[x])
				f[dfn[x]+j]=f[dfn[x]+j+1],f0[dfn[x]+j]=f0[dfn[x]+j+1];
		}
	}
	
	if (g[x]>Mx) Mx=g[x],Mxk=g0[x];
}

int solve(ll D){
	memset(f,0,sizeof(f));
	memset(g,0,sizeof(g));
	memset(f0,0,sizeof(f0));
	memset(g0,0,sizeof(g0));
	memset(tag,0,sizeof(tag));
	memset(tag0,0,sizeof(tag0));
	Mx=0,Mxk=0;
	dfs3(1,0,D);
	return Mxk;
}

int main(){
	freopen("tree.in","r",stdin);
	freopen("tree.out","w",stdout);
	scanf("%d%d%d",&n,&m,&K);
	ll s=0;
	for(i=1;i<=n;i++) scanf("%lld",&v[i]),s+=abs(v[i]);
	for(i=1;i<n;i++){
		scanf("%d%d",&x,&y);
		insert(x,y);
	}
	dfs(1,0);
	tot=0,fa[1]=1,dfs2(1,0);
	k=solve(0);
	if (k>m) l=-s,r=0; else
	if (k<m) l=0,r=s; else {
		printf("%lld",Mx);
		return 0;
	}
	while (l<r-1){
		mid=(l+r)/2;
		k=solve(mid);
		if (k>m) r=mid; else
		if (k<m) l=mid; else {
 			printf("%lld
",Mx-mid*m);
			return 0;
		}
	}
	solve(r);
	printf("%lld",Mx-r*m);
}