【NOIP2007】Hanoi双塔问题

题目描述

给定A、B、C三根足够长的细柱，在A柱上放有2n个中间有孔的圆盘，共有n个不同的尺寸，每个尺寸都有两个相同的圆盘，注意这两个圆盘是不加区分的（下图为n=3的情形）。

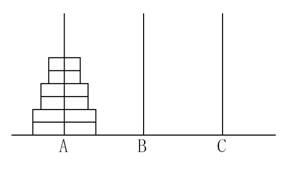
现要将这些圆盘移到C柱上，在移动过程中可放在B柱上暂存。要求：
（1）每次只能移动一个圆盘；
（2）A、B、C三根细柱上的圆盘都要保持上小下大的顺序；
任务：设An为2n个圆盘完成上述任务所需的最少移动次数，对于输入的n，输出An。

分析

思路简单一点，汉诺双塔=汉诺塔×2，OK，那么就是求两倍的汉诺塔，思路是一样的。
我们做一个比较简单的递推，要把2N个盘从A移动到B上，就先移动2(N-1)个到C上，在移2个到B上。
再把2(N-1)个移到B上，因此F(N)=2*F(N-1)+2
F(1)=2，易得F(N)=2^(N+1)-2
又因为N最大到200,2的201次方太大了，因此需要使用高精度。

AC代码

var
  a:array[1..100] of integer;
  n,i,j:integer;
begin
  fillchar(a,sizeof(a),0);         
  readln(n);
  a[1]:=1;                                                      
  for i:=1 to n+1 do
    begin
      for j:=1 to 100 do a[j]:=a[j]*2;
      for j:=2 to 100 do
        begin
          a[j]:=a[j]+a[j-1] div 10;
          a[j-1]:=a[j-1] mod 10;    
        end;
    end;                                    
  j:=100;
  while a[j]=0 do dec(j);            
  a[1]:=a[1]-2;
  for i:=j downto 1 do write(a[i]);
 end.