联考20200608 T1 Endless

题目：

分析：
原来平方串就是两个相同的串拼一起啊（大雾
考虑暴力的过程，将(K)种边按边权排序，暴力实现Kruskal算法
复杂度是(O(n^2))的
瓶颈就在于并查集
我们考虑培增，(f[k][x])表示([x,x+2^k))上的公共祖先，如果不在同一个并查集上，(f[k][x])指向(x)
这个只是为了方便判断，不含实际意义
求长度为(L)的平方串，我们可以把原串划分成长度为(L)的若干串，每次求出相邻两个串的LCP和LCS
LCP与LCS的相交部分，就是可以连边的中点范围
求LCP和LCS可以直接二分哈希

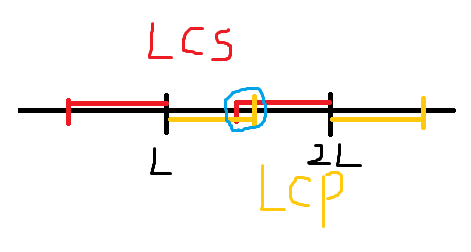
上图蓝色部分便是可以连边的中点范围
自己分析一下就可以发现以这些点为中点长度为(2L)的串是平方串
然后在倍增数组上连边，如果成功连边则往下继续连边，否则停止
由于(k)是(log)级别的，每一层最多连(O(n))条边，并查集平均单次复杂度(O(alpha(n)))
总复杂度(O(nlognalpha(n)))
具体的trick看代码吧

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<iostream>
#include<map>
#include<bitset>
#include<string>
#include<deque>

#define maxn 300005
#define INF 0x3f3f3f3f
#define base 998244353
#define MOD 1000000007

using namespace std;

inline long long getint()
{
	long long num=0,flag=1;char c;
	while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
	while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
	return num*flag;
}

int n,W;
int a[2*maxn];
int pw2[maxn],lg[maxn];
int hs[2*maxn],pw[2*maxn];
struct node{
	int w,L;
}q[maxn];
inline bool cmp(node x,node y){return x.w<y.w;}
int f[21][maxn];
long long ans;

inline int find(int k,int x){return f[k][x]==x?x:f[k][x]=find(k,f[k][x]);}

inline int getlcp(int x,int L)
{
	int l=0,r=L;
	while(l<r)
	{
		int mid=(l+r+1)>>1;
		if((hs[x+mid]-1ll*hs[x]*pw[mid]%MOD+MOD)%MOD==(hs[x+L+mid]-1ll*hs[x+L]*pw[mid]%MOD+MOD)%MOD)l=mid;
		else r=mid-1;
	}
	return l;
}
inline int getlcs(int x,int L)
{
	int l=0,r=L;
	while(l<r)
	{
		int mid=(l+r+1)>>1;
		if((hs[x]-1ll*hs[x-mid]*pw[mid]%MOD+MOD)%MOD==(hs[x+L]-1ll*hs[x+L-mid]*pw[mid]%MOD+MOD)%MOD)l=mid;
		else r=mid-1;
	}
	return l;
}

inline void merge(int x,int y,int k)
{
	int r1=find(k,x),r2=find(k,y);
	if(r1==r2)return;
	f[k][r1]=r2;
	if(!k){ans+=W;return;}
	merge(x,y,k-1),merge(x+pw2[k-1],y+pw2[k-1],k-1);
}

inline void work(int L,int R,int len)
{
	int k=lg[R-L+1];
	merge(L,L+len,k),merge(R-pw2[k]+1,R-pw2[k]+1+len,k);
}

inline void solve(int L)
{
	for(int i=L;i+L<=n;i+=L)
	{
		int tmp1=getlcp(i,L),tmp2=getlcs(i,L);
		if(tmp1+tmp2>=L)work(i-tmp2+1,i+tmp1,L);
	}
}

int main()
{
	int T=getint();
	pw2[0]=1;
	for(int i=1;i<=18;i++)pw2[i]=pw2[i-1]<<1,lg[pw2[i]]=i;
	for(int i=1;i<maxn;i++)lg[i]=max(lg[i],lg[i-1]);
	while(T--)
	{
		n=getint();ans=0;
		for(int j=0;j<=20;j++)for(int i=1;i<=2*n;i++)f[j][i]=i;
		for(int i=1;i<=n;i++)a[i]=getint();pw[0]=1;
		for(int i=n+1;i<=2*n;i++)a[i]=0;
		for(int i=1;i<=2*n;i++)hs[i]=(1ll*hs[i-1]*base+a[i])%MOD,pw[i]=1ll*pw[i-1]*base%MOD;
		for(int i=1;i<=n/2;i++)q[i].w=getint(),q[i].L=i;
		sort(q+1,q+n/2+1,cmp);
		for(int i=1;i<=n/2;i++)W=q[i].w,solve(q[i].L);
		printf("%lld
",ans);
	}
}