联考20200603 T2 排列

题目：

分析：
把排列看做一个(n)维上的点，(n!)个排列会在(n)维空间下构成一个凸包
如果输入的排列表示的点是在凸包上，那么就一定有解
什么玄学玩意？
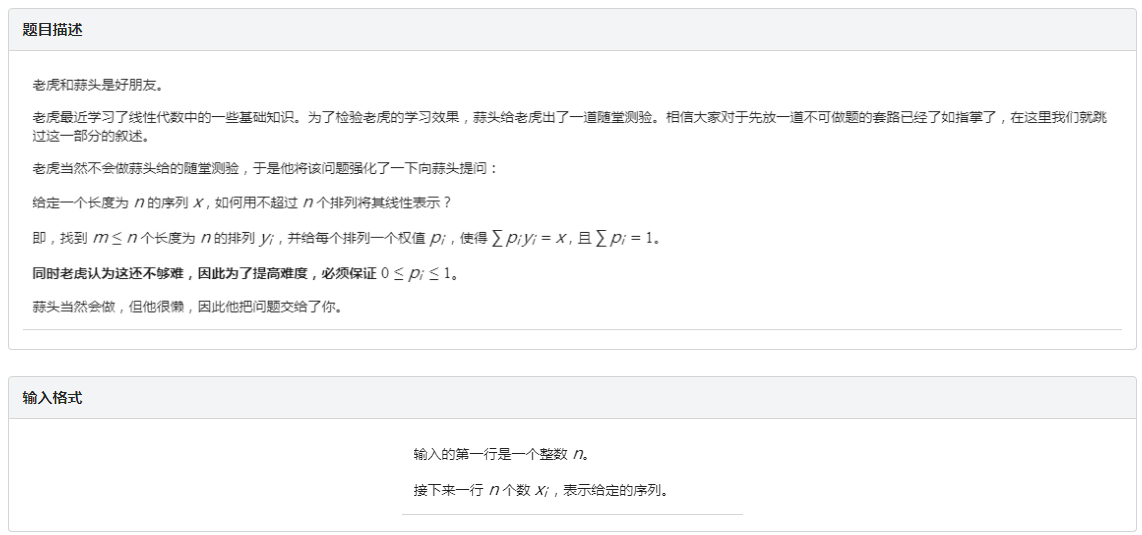
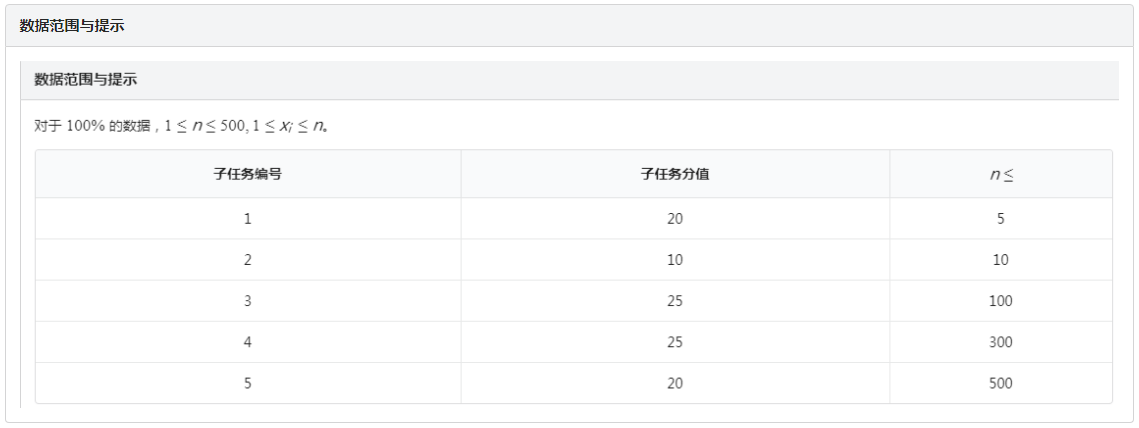
其实原序列为(X)，假设(X)从小到大排序后的序列为(Y)，如果有解，当且仅当满足下面两个条件：

(sum_{i=1}^{n}Y_i=frac{n(n+1)}{2})

(sum_{i=1}^{k}Y_igeq frac{k(k+1)}{2})

其中(k)为(1)到(n)的整数
冷静分析一下：
第一个式子由于(a_i=sum_{j=1}^{m}p_{j}b_{ij})，求和即可证明
转化到凸包上，每一个点到原点的曼哈顿距离都是(frac{n(n+1)}{2})，都可以用(n!)个排列形成的向量乘以模长(p)表示
第二个式子需要我们重新理解一下整个过程
我们可以将整个过程理解为，下标小的数需要下标大的数匀一些值过来，我们要求的便是匀过来值的占比
而如果一个前缀他自身需要的值比(frac{k(k+1)}{2})小，后面的数匀过来只会让它变大，无解
转化到凸包上，不合法的点会在凸包某一个(n-1)维的面上，但是不会再凸包上，无法表示

我们先把序列排序形成(Y)，用(1...n)的序列作为向量(a)乘以尽量长的(p)来表示
假设我们求出了一个(p)，向量(pa)从原点出发，终点假设为(A)
凸包上，每一个点到(A)的曼哈顿距离都是(frac{(1-p)n(n+1)}{2})，这个不难看出
那么原序列向量(Y)减去向量(pa)，然后从小到大排序得到的(Y')依然要满足：

(sum_{i=1}^{n}Y'_i=frac{(1-p)n(n+1)}{2})

(sum_{i=1}^{k}Y'_igeq frac{(1-p)k(k+1)}{2})

证明与上面同理
我们可以二分出最大的(p)，递归求解即可，由于每一次一定会有某一维达到瓶颈，我们最多只需要做(n)次

神仙题，可能讲不大清楚，先口胡这么长一段（
看代码可能能帮助理解

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<queue>
#include<iostream>
#include<map>
#include<bitset>
#include<string>

#define maxn 40005
#define INF 1<<30
#define eps 1e-13

using namespace std;

inline long long getint()
{
    long long num=0,flag=1;char c;
    while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
    while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
    return num*flag;
}

int n;
struct node{
	long double a;
	int id;
}A[maxn];
inline bool cmp(node x,node y){return x.a<y.a;}
long double B[maxn];
int sum;
int ans[maxn];

int main()
{
	n=getint();
	for(int i=1;i<=n;i++)
	{
		int x=getint();
		sum+=x,A[i].a=x;A[i].id=i;
	}
	if(sum!=n*(n+1)/2){puts("-1");return 0;}
	sort(A+1,A+n+1,cmp);
	long double num=0,now=1;
	for(int i=1;i<=n;i++)
	{
		num+=A[i].a;
		if(num<i*(i+1)/2){puts("-1");return 0;}
	}
	printf("%d
",n);
	for(int t=1;t<=n;t++)
	{
		sort(A+1,A+n+1,cmp);
		long double l=0,r=now;
		while(r-l>eps)
		{
			long double mid=(l+r)/2;bool flg=0;
			for(int i=1;i<=n;i++)
			{
				B[i]=A[i].a-mid*i;
				if(B[i]<-eps){flg=1;break;}
			}
			sort(B+1,B+n+1);
			long double num=0;
			for(int i=1;i<=n;i++)
			{
				num+=B[i];
				if(num+eps<(now-mid)*i*(i+1)/2){flg=1;break;}
			}
			if(flg)r=mid;
			else l=mid;
		}
		printf("%.12lf",(double)l);now-=l;
		for(int i=1;i<=n;i++)ans[A[i].id]=i,A[i].a-=l*i;
		for(int i=1;i<=n;i++)printf(" %d",ans[i]);
		printf("
");
	}
}