Leetcode #198 打家劫舍
题名:打家劫舍
描述:
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
具体描述请查看Leetcode相关网页:https://leetcode-cn.com/problems/house-robber/
方法:动态规划(递推)
偷到第 n 家后会有 F(n) 的金额,其中 F(n) = max( F(n - 2), F(n - 3) ) + nums[n - 1] (因为不能偷相邻人家的钱)
那么为什么只要比较第 F(n - 2) 和 F(n - 3) 就够了呢?不是还有 F(n - 4)、F(n - 5)..... 吗?
因为 F(n - 2) = max( F(n - 4), F(n - 5) ) + nums[n - 3] ; nums中存储的值必定大于等于0,所以 F(n - 2) >= max( F(n - 4), F(n - 5) ) ,同理
F(n - 3) >= max( F(n - 5), F(n - 6) );所以只要比较 F(n - 2) 和 F(n - 3) 就可以了~
代码如下:
//递推式: F(n) = max( F(n - 2), F(n - 3) ) + nums[n - 1];
int rob(vector<int>& nums) {
int n = nums.size();
if(n == 0) return 0;
if(n == 1) return nums[0];
if(n == 2) return max(nums[0], nums[1]);
if(n == 3) return max(nums[0] + nums[2], nums[1]);
// 从F(4) = max( F( 2 ), F( 1 ) ) + nums[3];开始递推
int ans, a = max(nums[0], nums[1]), b = nums[0],
c = max(nums[0] + nums[2], nums[1]);// a 用来存F(n - 2), b用来存F(n - 3), c用来存F(n - 1)
for(int i = 3;i < n;i++){
ans = max(a, b) + nums[i];
b = a;
a = c;
c = ans;
}
return max(ans, a);// 比较F(n)和F(n - 1),返回大的那个
Leetcode #213 打家劫舍 II
题名:打家劫舍 II
描述:
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
EXAMPLE1:
输入: [2,3,2]
输出: 3
解释: 你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
EXAMPEL2:
输入: [1,2,3,1]
输出: 4
解释: 你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
具体描述请查看Leetcode相关网页:https://leetcode-cn.com/problems/house-robber-ii/
在LeetCode #198的基础上多加了一个条件,也就是形成了一个环,要考虑最后一个元素和最前面的一个元素了。
环状排列意味着第一个房子和最后一个房子中只能选择一个偷窃,因此可以把此环状排列房间问题约化为两个单排排列房间子问题:
1.在不偷窃第一个房子的情况下(即 nums[1:]),最大金额是 p1;
2.在不偷窃最后一个房子的情况下(即 nums[:n-1]),最大金额是 p2;
**综合偷窃最大金额**: `max(p1, p2)`
作者:jyd
链接:https://leetcode-cn.com/problems/house-robber-ii/solution/213-da-jia-jie-she-iidong-tai-gui-hua-jie-gou-hua-/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
int rob(vector<int>& nums) {
int n = nums.size();
if(n == 0) return 0;
if(n == 1) return nums[0];
if(n == 2) return max(nums[0], nums[1]);
if(n == 3) return max(nums[0], max(nums[1], nums[2]));
int ans1 = max(nums[0] + nums[2], nums[1]),
ans2 = max(nums[1] + nums[3], nums[2]),
a = max(nums[0], nums[1]), b = nums[0],
c = ans1;
for(int i = 3;i < n - 1;i++){//计算nums[0:n - 1]
ans1 = max(a, b) + nums[i];
b = a;
a = c;
c = ans1;
}
ans1 = max(ans1, a);
a = max(nums[1], nums[2]);
b = nums[1];
c = max(nums[1] + nums[3], nums[2]);
for(int i = 3;i < n - 1;i++){//计算nums[1: ]
ans2 = max(a, b) + nums[i + 1];
b = a;
a = c;
c = ans2;
}
ans2 = max(ans2, a);
return max(ans1, ans2);
}
hdoj #2084 数塔
题名:数塔
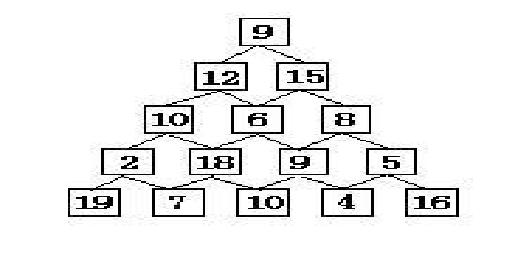
描述:
Input
输入数据首先包括一个整数C,表示测试实例的个数,每个测试实例的第一行是一个整数N(1 <= N <= 100),表示数塔的高度,接下来用N行数字表示数塔,其中第i行有个i个整数,且所有的整数均在区间[0,99]内。
Output
对于每个测试实例,输出可能得到的最大和,每个实例的输出占一行。
EXAMPLE
input:
1
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
output:
30
方法:DP
从顶层往下递推,将a[i]j加上,上一次相邻的最大值max(a[i-1][j-1], a[i-1][j]),当然要判断a[i-1][j-1]不存在的情况,也就是j = 0的情况;
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
对第二行做上述操作后:
7
10 15
8 1 0
2 7 4 4
4 5 2 6 5
对第三行做上述操作后:
7
10 15
18 16 15
2 7 4 4
4 5 2 6 5
依次迭代,最后一行的最大值即为答案;
代码如下:
#include <iostream>
#include <algorithm>
using namespace std;
int main(){
int n;
cin>>n;
while(n--){
int m;
cin>>m;
int a[m][m];
// fill(a[0], a[0] + m * m, 0);
for(int i = 0;i < m;i++){
for(int j = 0;j < m;j++){
a[i][j] = 0;
}
}
for(int i = 0;i < m;i++){
for(int j = 0;j <= i;j++){
int tmp;
cin>>tmp;
a[i][j] = tmp;
}
}
for(int i = 1;i < m;i++){
for(int j = 0;j <= i;j++){
if(j > 0)
a[i][j] += max(a[i - 1][j - 1], a[i - 1][j]);
else
a[i][j] += a[i - 1][j];
}
}
int ans = 0;
for(int i = 0;i < m;i++){
if(a[m - 1][i] > ans)
ans = a[m - 1][i];
}
printf("%d
", ans);
}
return 0;
}
Leetcode #42 接雨水
题名:接雨水
描述:
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6
具体描述请查看Leetcode相关网页:https://leetcode-cn.com/problems/house-robber-ii/
方法一:暴力法
0.因为第一个柱子和最后一根柱子上面不可能积水,所以从柱子从第2根开始到倒数第二根。
1.从第2个柱子开始,指定一个柱子i,找到在它左边最高的那个柱子的高度max_left和在它右边最高的那个柱子的高度max_right,得到两者的较小的那个 min(max_left, max_right)的高度h,如果这个高度h大于柱子i的高度,那么柱子i上需要加入h - i单位的水;
2.重复第1步,直到倒数第二个柱子。
代码如下:
int trap(vector<int>& height) {
int i, ans = 0, end = height.size();
for(i = 1;i < end - 1;i++){//从第2根开始到倒数第二根
int max_left = 0, max_right = 0;
for(int x = i;x >= 0;x--){
max_left = max(max_left, height[x]);
}
for(int y = i;y < end;y++){
max_right = max(max_right, height[y]);
}
int min_wall = min(max_left, max_right);
ans += min_wall - height[i];
}
return ans;
}