一、卡特兰数(Catalan number)
1.定义
组合数学中一个常出现在各种计数问题中出现的数列(用c表示)。以比利时的数学家欧仁·查理·卡特兰的名字来命名;
2.计算公式
(1)递推公式
c[n]=Σ(0≤k<n)c[k]c[n-k-1],边界条件为c[0]=1;
其递推解为c[n]=C(2n,n)/(n+1),即卡特兰数的通项公式,其中C表示数的组合;
根据组合公式我们可以化简得c[n]=2n(2n-1).....(n+2)/n!;
(2)另类递推式
c[n]=c[n-1](4n-2)/(n+1),边界条件为c[0]=1;
其递推解为c[n]=C(2n,n)-C(2n,n-1),C表示数的组合;
(3)其他公式
c[n]=(Σ(0≤i≤n)C(i,n)^2)/(n+1);
ps:通过展开可以发现它们的本质是一样的;
3.简单应用
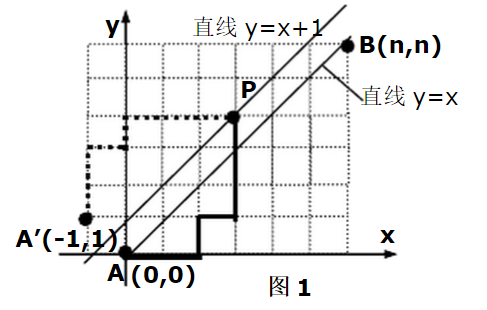
(1)求解路径方案数:如图所示,从原点(0,0)到点B(n,n),只能向右或向上进行长度为一个单位的移动,路线一直处于y=x之下(不越过直线y=x)的不同路径方案数;
Solution:每个n的解都可以看做先前的解数(再向右向上即为所求)加上不触及各个y=x上的点到达B点的方案数,可以发现其递推公式即为卡特兰数计算公式;
(2)求01串的个数:n个0与n个1构成的序列方案数,使得任何一个前缀0的个数不少于1的个数;
Solution:将0看做在坐标系中向右走一步,1看做向上走一步,则问题可化简为从原点到(n,n)所有路线中一直处于y=x之下(不越过直线y=x)的不同路径方案数,与上题相同,方案数即为对应n的卡特兰数;
(3)给定节点求解二叉树的个数:已知由n个节点,求形成不同的二叉树有多少种?
Solution:将向左生成子树看做0,向右生成字数看成1,则问题化简为求n/2个0和n/2个1构成数串的不同方案数,即上题无条件解的一半,与上题答案相同,形成不同的树的个数即为对应n的卡特兰数;
(4)求凸边形进行三角剖分的不同方案数:在一个有n+3条边的凸多边形中,求通过若干条互不相交的对角线,把这个多边形划分成若干个三角形的不同方案数。
Solution:因为每一条边都一定是剖分后的三角形的一条边,任意一条边都会把多边形分成两个小多边形,那么根据乘法原理,解即为划分成不同多边形的方案数对应小多边形的划分方案数之和,即f[n]=Σ(3≤k≤n-3)f[k]f[n-k-1],可以发现解数即为n对应的卡特兰数;
(5)n对括号正确匹配数目:给定n对括号,求括号正确配对的字符串数;
Solution:因为是匹配问题,那么最后一个左括号必然有唯一右括号与其匹配,假设f[n]为n对括号的正确配对数目,那么有递推关系f[n]=f[0]f[n-1]+f[1]f[n-2]+...+f[n-1]f[0],显然f[n]是n对应的卡特兰数。
4.卡特兰数的扩展(折线原理)
对于在n位的2进制中,有m个0,其余为1的catalan数为:C(n,m)-C(n,m-1)。其可由应用(1)证明;
二、相关应用
1.[NOIP2003]栈
题解随笔:http://www.cnblogs.com/COLIN-LIGHTNING/p/8481413.html
2.[洛谷P1722]矩阵II
Description
给定一个长度为2n的数列,现让你自由地放入红色算筹和黑色算筹,求对于所有的i(1<=i<=2n),使第1~i格中红色算筹个数大于等于黑色算筹的方案数;
输入:n
输出:对100取模后的方案数;
Solution
1.将红看做入栈操作,黑看为出栈操作,问题即为求不同的合法的入栈出栈序个数;
2.那么解法与上题相同,易得解即为对应的卡特兰数;
3.我们可以考虑用递推式(1)求卡特兰数,取模更容易;
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
int main(){
unsigned long long ctl[110],i,j,k,n;
memset(ctl,0,sizeof(ctl));
ctl[0]=ctl[1]=1;
ctl[2]=2;
scanf("%d",&n);
for(i=3;i<=n;++i)
for(j=0;j<i;++j){
ctl[i]+=ctl[j]*ctl[i-j-1];
ctl[i]%=100;
}
printf("%d
",ctl[n]);
return 0;
}
3.[洛谷P1976]鸡蛋饼
Description
最近小 x 又发现了一个关于圆的有趣的问题:在圆上有2N 个不同的点,小 x 想用 N 条线段把这些点连接起来(每个点只能连一条线段), 使所有的线段都不想交,他想知道这样的连接方案有多少种?
输入输出格式
输入格式:有且仅有一个正整数 N
输出格式:要求的方案数(结果 mod 100000007)。
Solution
1.可将问题化简为求n+3边形进行三角剖分的方案数,解法就显而易见了;
2.对1e8+7取模可以考虑使用递推公式(1)解决;
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
int main(){
unsigned long long ctl[32768],i,j,k,n;
memset(ctl,0,sizeof(ctl));
ctl[0]=ctl[1]=1;
ctl[2]=2;
scanf("%d",&n);
for(i=3;i<=n;++i)
for(j=0;j<i;++j){
ctl[i]+=ctl[j]*ctl[i-j-1];
ctl[i]%=100000007;
}
printf("%d
",ctl[n]);
return 0;
}