3、调整偏移量伪指令
调整偏移量伪指令是在内存变量定义时用来调整内存变量起始偏移量的,它们是在把源程序汇编成目标文件时起作用。常用的调整偏移量伪指令有:EVEN、ALIGN和ORG,它们的主要目的是:为了更有效地读取内存单元的内容。
(1)偶对齐伪指令EVEN
偶对齐伪指令格式:EVEN
伪指令的作用是:告诉汇编程序(Assember),本伪指令下面的内存变量从下一个偶地址单元开始分配。
如果下一个偏移量是偶地址,那么,该伪指令不起作用,否则,汇编程序将空出一个字节,从下一偶地址开始为其后变量分配内存单元。
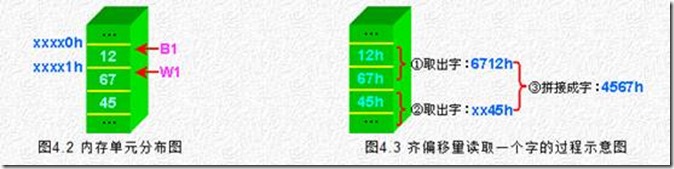
假设有下列变量定义,并且变量B1的偏移量是偶数,其内存单元分布如图4.2所示。
B1 DB 12H ;为了表示方便,不妨再假设其偏移量为:xxxx0H
W1 DW 4567H
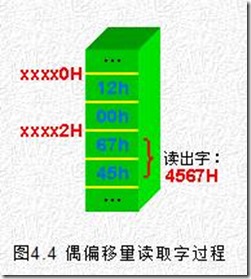
在上述定义情况下,在许多微机系统中,当需要读变量W1及其后面的字内容时,硬件将按图4.3所示的方式分二次读出该字内容,再拼接成一个字内容,这时,无疑需要二个读内存周期,从而影响程序执行的速度。
出现上述问题的主要原因就是字变量W1在数据段内的偏移量是奇数,为了保证其偏移量是偶数,需要在其定义之前加上伪指令EVEN。
所以,可把前面的变量定义改变成下列形式:
B1 DB 12H
EVEN
W1 DW 4567H
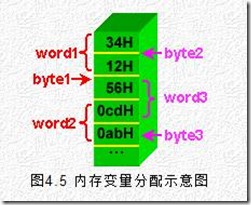
这时,变量的内存分配和读取字变量W1的过程如图4.4所示。
(2)对齐伪指令ALIGN
对齐伪指令格式:
ALIGN Num
其中:Num必须是2的幂,如:2、4、8和16等。
伪指令的作用是:告诉汇编程序,本伪指令下面的内存变量必须从下一个能被Num整除的地址开始分配。
如果下一个地址正好能被Num整除,那么,该伪指令不起作用,否则,汇编程序将空出若干个字节,直到下一个地址能被Num整除为止。
试比较下面二组变量定义,它们的对齐效果一致吗?
B1 DB 12H B1 DB 12H
EVEN ALIGN 2
W1 DW 4567H W1 DW 4567H
从上面的对比,我们不难看出:伪指令ALIGN的说明功能要比伪指令EVEN强。
(3)调整偏移量伪指令ORG
调整偏移量伪指令格式:
ORG 数值表达式
伪指令的作用是:告诉汇编程序,本伪指令下面的内存变量从该“数值表达式”所指定的地址开始分配。
假设有下列变量定义,并且变量word1的偏移量为0。
word1 DW 1234h
byte1 DB 56h
word2 DW 0abcdh
ORG 1
byte2 DB ?
word3 DW ?
byte3 DB ?
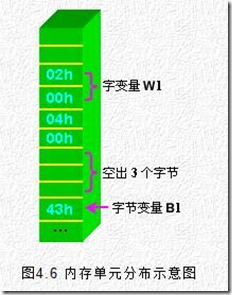
前三个变量定义的内存分布如图4.5的左边所示,但由于伪指令“ORG 1”的作用,说明其后面所说明的变量要从偏移量为“1”的内存单元开始存放。所以,后三个变量的内存分配如图4.5的右边所示。
由图4.5可见,这些变量的内存分配是相互重叠的,对某个变量的操作无疑会影响到与之重叠的变量。
另外,变量byte2、word3和byte3没有赋初值,如果赋初值的话,则重叠部分的内存单元的原来初值将被覆盖掉。
在以上三个伪指令EVEN、ALIGN和ORG中,伪指令EVEN的使用频率较高。
(4)偏移量计数器的值
前面,我们介绍了几种改变偏移量计数器之值的方法,但在程序中还无法引用其值。汇编语言提供了一个特殊的符号“$”来引用偏移量计数器的值。
例如:
W1 DW $, $
ORG $+3 ;从当前地址开始空3个字节
B1 DB 43h
假设:在给变量W1分配内存单元时,当前偏移量计数器的值为2。
于是,变量W1后面第一个“$”代表数值2,第一个字分配后,此时偏移量计数器$的值就为4,所以,第二个“$”就代表数值4。
在分配完二个字之后,偏移量计数器的值变为6,$+3的值为9,所以,伪指令“ORG $+3”就表示下一个变量从偏移量为9的单元地址开始分配。
综上分析,上述变量说明所对应的内存单元分布如图4.6所示。