#3 CF536D & CF538G & CF559E

没想到吧辣鸡博主竟然还能更。

Tavas in Kansas

题目描述

点此看题

解法

可以把原问题抽象出来，每个点具有两个特征值 \((a_i,b_i)\)，分别表示和两个玩家的距离，因为每个玩家的 \(x\) 都是递增的，所以可以设计状态 \(dp[0/1][x][y]\) 表示现在是先手\(/\)后手操作，先后手分别去到了 \(x,y\)，此时差值是多少。

暴力转移要枚举转移点。但其实每次可以只把 \(x\) 增大 \(1\)（\(y\) 同理），然后如果增大导致了点的选取，那么可以从 \(dp[0][x+1][y]/dp[1][x+1][y]\) 转移而来；否则只能从 \(dp[0][x+1][y]\) 转移而来，因为必须选取所以要继续增大。

那么跑完最短路之后把距离离散化一下就可以了，时间复杂度 \(O(n^2)\)

#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
const int M = 2005;
#define int long long
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,x,y,tot,f[M],a[M],b[M],c[M],dis[M];
int w[M],sum[M][M],siz[M][M],dp[2][M][M];
struct edge{int v,c,next;}e[M<<8];
struct node
{
	int u,c;
	bool operator < (const node &b) const {return c>b.c;}
};
void dijk(int s,int *a)
{
	priority_queue<node> q;
	for(int i=1;i<=n;i++) dis[i]=1e18;
	q.push(node{s,0});dis[s]=0;
	while(!q.empty())
	{
		int u=q.top().u,w=q.top().c;q.pop();
		if(dis[u]<w) continue;
		for(int i=f[u];i;i=e[i].next)
		{
			int v=e[i].v,c=e[i].c;
			if(dis[v]>dis[u]+c)
			{
				dis[v]=dis[u]+c;
				q.push(node{v,c}); 
			}
		}
	}
	for(int i=1;i<=n;i++) c[i]=dis[i];
	sort(c+1,c+1+n);
	for(int i=1;i<=n;i++)
		a[i]=lower_bound(c+1,c+1+n,dis[i])-c;
}
int calc(int xl,int yl,int xr,int yr)
{
	return sum[xr][yr]-sum[xl-1][yr]-sum[xr][yl-1]+sum[xl-1][yl-1];
}
int sz(int xl,int yl,int xr,int yr)
{
	return siz[xr][yr]-siz[xl-1][yr]-siz[xr][yl-1]+siz[xl-1][yl-1];
}
signed main()
{
	n=read();m=read();x=read();y=read();
	for(int i=1;i<=n;i++) w[i]=read();
	for(int i=1;i<=m;i++)
	{
		int u=read(),v=read(),c=read();
		e[++tot]=edge{v,c,f[u]},f[u]=tot;
		e[++tot]=edge{u,c,f[v]},f[v]=tot;
	}
	dijk(x,a);dijk(y,b);
	for(int i=1;i<=n;i++)
		sum[a[i]][b[i]]+=w[i],siz[a[i]][b[i]]++;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		{
			sum[i][j]+=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
			siz[i][j]+=siz[i-1][j]+siz[i][j-1]-siz[i-1][j-1];
		}
	for(int i=n;i>=1;i--)
		for(int j=n;j>=1;j--)
		{
			if(sz(i,j,i,n)>0)
				dp[0][i][j]=max(dp[0][i+1][j],dp[1][i+1][j])+calc(i,j,i,n);
			else dp[0][i][j]=dp[0][i+1][j];
			if(sz(i,j,n,j)>0)
				dp[1][i][j]=min(dp[1][i][j+1],dp[0][i][j+1])-calc(i,j,n,j);
			else dp[1][i][j]=dp[1][i][j+1];
		}
	if(dp[0][1][1]>0) puts("Break a heart");
	else if(dp[0][1][1]<0) puts("Cry");
	else puts("Flowers");
}

Berserk Robot

题目描述

点此看题

解法

博主是个伞兵可以拖出去喂鱼了，但是本题确实是完全可做的，本题的所有思路都是有据的。

高维问题可以考虑拆分成独立的低维问题，我们可以把坐标系旋转 \(45\) 度，那么 U,R,D,L 就分别是 \((1,1),(1,-1),(-1,-1),(-1,1)\)，可以再化成 \(\{0,1\}\) 的形式，我们让 \(x'=\frac{x+y+t}{2},y'=\frac{y-x+t}{2}\)，那么它们就分别代表 \((1,1),(1,0),(0,0),(0,1)\)，如果修改坐标轴之后出现了非整数坐标那么就说明无解。

设 \(s_i\) 表示时刻 \(i\) 的位移，\(v=s_l\) 表示一个周期的位移，\(k_i=\lfloor\frac{t_i}{l}\rfloor\) 表示周期数，\(w_i=t_i\bmod l\) 表示多出来的前缀长度。可以列出如下关系式：\((x_i,y_i)=s_i=k_i\cdot v+s_{w_i}\)，这样的关系式一共有 \(n\) 个，且可以用 \((x_i,y_i,k_i,w_i)\) 的四元组表述。

观察到如果我们确定 \(v\) 就可以确定所有 \(s_{w_i}\)，老样子我们先找必要条件。我们先考虑 \(v_x\) 的范围，为了方便我们新增 \((0,0)=0\cdot v+s_0,(0,0)=-1\cdot v+s_{l}\)，然后把所有关系按照 \(w_i\) 排序之后差分：

\[x_j-x_i=(k_j-k_i)\cdot v_x+(s_{w_i}-s_{w_j})_x \]

设 \(k=k_j-k_i,w=w_i-w_j\)，我们可以利用 \(0\leq (s_{w_j}-s_{w_i})\leq w\) 来列不等式：

\[x_j-x_i-w\leq k\cdot v_x\leq x_j-x_i \]

解这个不等式是很简单的，只需要按照 \(k\) 和 \(0\) 的关系分类讨论即可：

• 若 \(k=0\)，需要满足 \(x_j-x_i\leq 0\leq x_j-x_i+w\)
• 若 \(k>0\)，需要满足 \(\lceil\frac{x_j-x_i-w}{k}\rceil\leq v_x\leq \lfloor\frac{x_j-x_i}{k}\rfloor\)
• 若 \(k<0\)，需要满足 \(\lceil\frac{x_j-x_i}{k}\rceil\leq v_x\leq \lfloor\frac{x_j-x_i-w}{k}\rfloor\)

那么很容易就能解出 \(v_x\) 的范围并判断无解，那么我们尝试构造原序列。

我们可以先算出所有的 \(s_{w_i}\)，发现 \(w_i\) 把原序列划分成了很多段，那么对于每一段我们算出 \(x,y\) 的差值，然后就根据这个来填字符即可。为什么这样构造一定有解呢？因为我们的必要条件就保证了 \(0\leq (s_{w_j}-s_{w_i})\leq w\)，也就是这一段的差值一定可以通过 \(1\) 来填上，这也应证了我们为什么要通过差分来列式，因为我们想让每一小段都满足条件。

总结

如果想要构造等式的解，可以先观察等式的数量，然后找到统摄全局等式的变量。必要条件可以通过列不等式来获得，想要获得强力的必要条件需要对等式做一些变换（比如差分）

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int M = 200005;
#define int long long
#define Morisummer {puts("NO");return 0;}
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,lx,rx,ly,ry;
struct node
{
	int x,y,k,w;
	bool operator < (const node &b) const
	{return w<b.w;}
}p[M];
signed main()
{
	n=read();m=read();
	lx=ly=-9e18;rx=ry=9e18;
	for(int i=1;i<=n;i++)
	{
		int t=read(),x=read(),y=read();
		if((t^x^y)&1) Morisummer
		p[i].k=t/m;p[i].w=t%m;
		p[i].x=(x+y+t)/2;p[i].y=(y-x+t)/2;
	}
	p[++n].w=m;p[n].k=-1;
	sort(p+1,p+1+n);
	for(int i=1;i<=n;i++)
	{
		int k=p[i].k-p[i-1].k;
		int w=p[i].w-p[i-1].w;
		int dx=p[i].x-p[i-1].x;
		int dy=p[i].y-p[i-1].y;
		if(!k)
		{
			if(dx-w>0 || dx<0) Morisummer
			if(dy-w>0 || dy<0) Morisummer
		}
		else if(k>0)
		{
			lx=max(lx,(int)ceil(1.0L*(dx-w)/k));
			rx=min(rx,(int)floor(1.0L*dx/k));
			ly=max(ly,(int)ceil(1.0L*(dy-w)/k));
			ry=min(ry,(int)floor(1.0L*dy/k));
		}
		else
		{
			k*=-1;
			lx=max(lx,(int)ceil(1.0L*(-dx)/k));
			rx=min(rx,(int)floor(1.0L*(-dx+w)/k));
			ly=max(ly,(int)ceil(1.0L*(-dy)/k));
			ry=min(ry,(int)floor(1.0L*(-dy+w)/k));
		}
	}
	if(lx>rx || ly>ry) Morisummer
	for(int i=1;i<=n;i++)
	{
		int dx=(p[i].x-p[i].k*lx)-(p[i-1].x-p[i-1].k*lx);
		int dy=(p[i].y-p[i].k*ly)-(p[i-1].y-p[i-1].k*ly);
		int w=p[i].w-p[i-1].w;
		while(w--)
		{
			if(dx>0)
			{
				dx--;
				if(dy>0) putchar('U'),dy--;
				else putchar('R');
			}
			else
			{
				if(dy>0) putchar('L'),dy--;
				else putchar('D');
			}
		}
	}
	puts("");
}

Gerald and Path

题目描述

点此看题

解法1

其实本题的最难点是 \(n\leq 100\)，这种反向提示时间复杂度真的让人很难受。

设 \(f[i][j][0/1]\) 表示考虑前 \(i\) 个线段，在右端点最靠右的线段是 \(j\)，它的朝向是左\(/\)右，所得到的最大覆盖长度。转移可以先考虑 \(i\) 到 \(i+1\)，那么我们考虑线段 \(i+1\) 和线段 \(j\) 的关系来计算贡献。

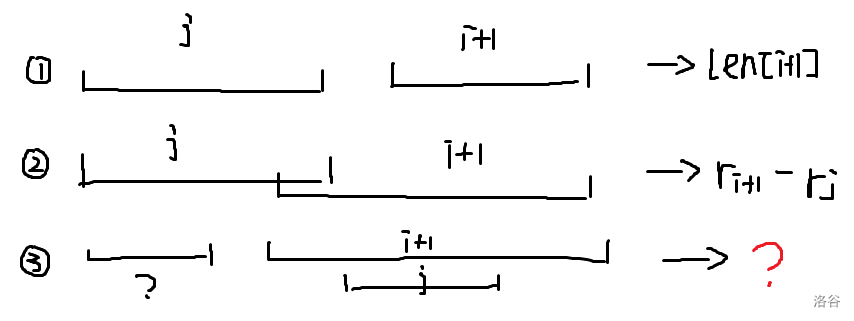
上图展示了 \(i\) 和 \(j\) 关系的讨论，如果 \(j\) 产生贡献的情况那么 \(i+1\) 的新增贡献很好计算。但是如果 \(i\) 包含 \(j\)，我们就会用到前面一些不可知的信息，这样贡献是怎么都算不对的。

上面的思考还是反应出一个底层问题：由于这道题覆盖多次只计入单次贡献，所以转移顺序不能混乱。那么从转移顺序的角度思考，如果 \(j\) 在之后不产生贡献，我们可以在之前就忽略它，但是忽略操作不能乱做，是需要枚举法的。

具体来说考虑 \(i\) 转移到 \(k\)，我们把 \(j,k\) 按照 \(\min(len_k,r_k-r_j)\) 计算贡献，然后我们把 \([i+1,k-1]\) 这些线段在线段 \(k\) 范围内的贡献忽略，也就是钦定它们的方向，只计算越过 \(k\) 的那一段的贡献。考虑上面这步可能会导致贡献算少，但是如果算少发现一定不优，且最优解是一定会被统计到的，所以不用多去关心。

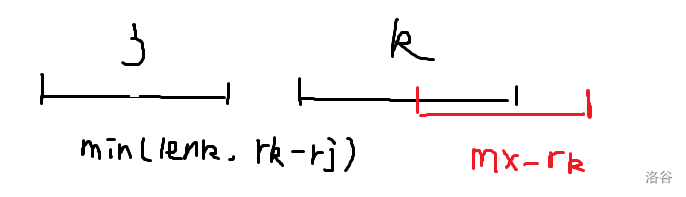
那么 \(k\) 从 \(i+1\) 枚举到 \(n\)，过程中维护 \([i+1,k-1]\) 延伸出最远的线段即可，时间复杂度 \(O(n^3)\)，上面讨论的是 \(j,k\) 都朝左的情况，其他的情况类似分析一下就可以了，建议看代码。

解法2

这老哥真的牛逼，我做过 lanterns 都没有任何想法，直接给我类比出来了。

我们先把 \(a_i-b_i,a_i,a_i+b_i\) 这些位置都离散化，考虑最终点亮的情况一定是若干个不交的段，那么我们直接规划这些段即可，那么转移的关键就变成了判定段是否合法，考虑用上一题的方法求出 \(g_{l,r}\) 表示用点 \([l,r]\) 之间的线段是否能覆盖 \([l,r]\) 这些点，然后设 \(f_i\) 表示考虑前 \(i\) 个点的答案：

\[f_i=\max(f_{j-1}+s_i-s_j) \]

转移条件是 \(g_{j,i}\) 为真，其中 \(s_i\) 表示离散化之后第 \(i\) 个点的坐标，时间复杂度 \(O(n^2\log n)\)

解法3

如果说解法 \(2\) 还是生搬硬套了点，那么解法 \(3\) 就真的是神来之笔了，\(\tt OUYE\) 永远的神！！

首先还是离散化，原来我们是被覆盖的区间计入一次贡献，现在我们考虑不被覆盖的点付出代价，那么相当于可以付出 \(p_{i+1}-p_i\) 的代价使用 \([i,i+1]\) 的线段，要求最小的代价把所有点都覆盖完。

设 \(dp[i][j]\) 表示使用前 \(i\) 个点的线段覆盖了长度为 \(j\) 的前缀的最小代价。如果这个位置有线段，转移考虑讨论线段向左覆盖还是向右覆盖。如果线段向右覆盖，则有：

\[dp[i][r_i]\leftarrow dp[i-1][k],i\leq k<r_i \]

线段向左覆盖貌似不是很好做，可以再记 \(f[i][j]\) 表示再 \(dp[i][j]\) 的基础上线段 \(i\) 是向左倒的，那么我们可以枚举之前的一个线段 \(j\) 向左倒，使得 \(l_j\leq l_i\)，也就是 \(l_i\) 在子问题中的影响完全被取消了，设 \(mr=\max(i,\max_{j<k<i} r_k)\)那么有转移：

\[f[i][mr]\leftarrow f[j][k],j\leq k< mr \]

也可能 \(i\) 覆盖的范围中没有线段向左，那么此时直接就得到子问题了：

\[f[i][mr]\leftarrow f[l_i][j],l_i\leq j< mr \]

最后一种转移就是使用需要代价的线段：

\[dp[i][i]\leftarrow dp[i-1][i-1]+p_i-p_{i-1} \]

发现优化复杂度的关键是第二个转移，但是我们把 \(f[i]\) 弄个前缀 \(\min\) 就可以优化了，时间复杂度 \(O(n^2)\)，实现可能相较于上面讲的东西有一点微调，可以看看代码。

总结

思考转移顺序十分重要，忽略思想是让贡献顺序正确的重要方法。

统计一些不正确但是一定不优的情况可能让转移更加简单。

思考最后答案的形式，可能会帮助你把最优化问题转化为判定问题。

寻找子问题要考虑消除后面操作的影响。

//O(n^3)
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int M = 105;
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,ans,f[M][M][2];
struct node
{
	int x,y;
	bool operator < (const node &b) const
	{return x<b.x;}
}a[M];
void upd(int &x,int y) {x=max(x,y);}
signed main()
{
	n=read();
	for(int i=1;i<=n;i++)
		a[i].x=read(),a[i].y=read();
	sort(a+1,a+1+n);a[0].x=-1e9;
	for(int i=0;i<=n;i++)
	for(int j=0;j<=i;j++)
	for(int p=0;p<2;p++)
	{
		ans=max(ans,f[i][j][p]);
		int o=a[j].x+p*a[j].y,mx=-1e9,x,y;
		for(int k=i+1;k<=n;k++)
		for(int q=0;q<2;q++)
		{
			int t=a[k].x+q*a[k].y;
			if(t>mx) mx=t,x=k,y=q;
			upd(f[k][x][y],f[i][j][p]
			+min(a[k].y,t-o)+mx-t);
		}
	}
	printf("%d\n",ans);
}

//O(n^2)
#include <cstdio>
#include <algorithm>
using namespace std;
const int M = 1005;
const int inf = 0x3f3f3f3f;
int read()
{
	int x=0,f=1;char c;
	while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
	while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int n,m,a[M],b[M],p[M],L[M],R[M],f[M][M],dp[M][M];
void upd(int &x,int y) {x=min(x,y);}
signed main()
{
	n=read();
	for(int i=1;i<=n;i++)
	{
		a[i]=read();b[i]=read();
		p[++m]=a[i]-b[i];p[++m]=a[i];p[++m]=a[i]+b[i];
	}
	sort(p+1,p+1+m);m=unique(p+1,p+1+m)-p-1;
	for(int i=1;i<=n;i++)
	{
		int x=lower_bound(p+1,p+1+m,a[i])-p;
		L[x]=lower_bound(p+1,p+1+m,a[i]-b[i])-p;
		R[x]=lower_bound(p+1,p+1+m,a[i]+b[i])-p;
	}
	for(int i=0;i<=m;i++)
		for(int j=0;j<=m;j++)
			f[i][j]=dp[i][j]=inf;
	dp[1][1]=0;
	for(int i=1;i<=m;i++)
	{
		if(L[i])
		{
			int mr=i;
			for(int j=i-1;j>L[i];j--) if(L[j])
			{
				if(L[j]<=L[i]) upd(f[i][mr],f[j][mr]);
				mr=max(mr,R[j]);
			}
			for(int j=L[i];j<=mr;j++)
				upd(f[i][mr],dp[L[i]][j]);
			//seg i ->
			for(int j=i;j<R[i];j++)
				upd(dp[i][R[i]],dp[i][j]);
			//seg i <-
			for(int j=i;j<=m;j++)
				upd(dp[i][j],f[i][j]);
		}
		for(int j=i+1;j<=m;j++) upd(dp[i+1][j],dp[i][j]);
		upd(dp[i+1][i+1],dp[i][i]+p[i+1]-p[i]);
		for(int j=i+1;j<=m;j++) upd(f[i][j],f[i][j-1]);
	}
	printf("%d\n",p[m]-p[1]-dp[m][m]);
}