时间复杂度入门理解

前言

---

　　当你编写完一个程序的时候，怎样对它进行算法最优的判断呢？效率又是怎样体现的呢？效率=总执行次数/总时间，一般来说，程序越庞大，其执行效率越低。因此，对于模块化程序，优化其算法的时间复杂度是非常重要的。

　　 

定义

---

　　我们把一个算法中的语句执行次数定义为频度，算法的运行时间刻画为一个函数，定义为 T(n) ，其中n称为问题的规模，当n不断变化时，T(n)也随之变化。但我们想知道n与T(n)之间的大致规律，所以我们引入渐进符号 O 来刻画算法的运行时间。

　　现在我们编写一个程序，把其中表示算法运行时间的函数记为 T(n)。对于一个给定的函数 g(n)，有 O(g(n)) = {f(n) | 存在常量 c, n₀, c>0, n₀>0, 使得对所有 n ≥ n₀, 有0  ≤ f(n)  ≤ c·g(n)}，记作 f(n) = O(g(n)) 。如下图。注意这个等号并不是左右相等，而是代表集合论中的 “∈”，表示 'is a ..' 的关系，如“ n = O(n²) ”。当我们说运行时间为 O(g(n)) 时，表示存在一个O(g(n)) 的函数 f(n)，使得 n 不管输入什么值时，T(n) 的上界都是 f(n)。所以 O(g(n)) 表示最坏情况运行时间。

　　通常,我们称 O(g(n)) 为时间复杂度。

　　

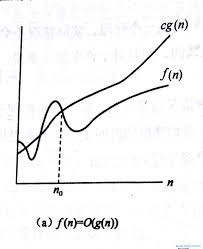
　　　　　　图(a) f(n) = O(g(n))  

按增长量级递增排列，常见的时间复杂度有：

常数阶O(1),  对数阶O(log2n),  线性阶O(n),  线性对数阶O(nlog2n),  平方阶O(n^2)， 立方阶O(n^3),...， k次方阶O(n^k), 指数阶O(2^n) 。

　　　　

 计算时间复杂度

---

 

粗略地计算的话就知道以下三步即可：

     

　 1.去掉运行时间中的所有加法常数。

     2.只保留最高阶项。

     3.如果最高阶项存在且不是1，去掉与这个最高阶相乘的常数得到时间复杂度

我们看一个例子

 for (int i = 0; i < n; i++) {

          for (int j = i; j < n; j++) {

               // do .....

          }

     }

　　

当 i = 0 时 里面的for循环执行了n次，当i等待1时里面的for循环执行了n -  1次，当i 等于2里里面的fro执行了n - 2次........这样，就可以将循环对应成等差数列，项数为最外层循环的次数，公差为1,首项是i = 0  or  i = n-1 时内层循环的执行次数，末项是i = n-1  or  i = 0 时的内层循环的执行次数所以执行的次数是

那么得到运行时间的函数   （c 是常数）

根据我们上边的时间复杂度算法

     1.去掉运行时间中的所有加法常数： 没有加法常数不用考虑

     2.只保留最高阶项:　只保留 

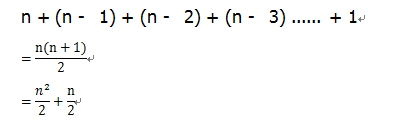
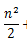
     3. 去掉与这个最高阶相乘的常数:  去掉只剩下 

     最终这个算法的时间复杂度为

 

 下面拿几道题练练手：

(1)

 for(i=1;i<=n;i++)   
            for(j=1;j<=n;j++)
                 s++;

//循环了n*n次，当然是O(n^2)

(2)

     for(i=1;i<=n;i++)
            for(j=i;j<=n;j++)
                 s++;
    
    //循环了(n+n-1+n-2+...+1)≈(n^2)/2，因为时间复杂度是不考虑系数的，所以也是O(n^2)

(3)

  for(i=1;i<=n;i++)
            for(j=1;j<=i;j++)
                 s++;

//循环了(1+2+3+...+n)≈(n^2)/2,当然也是O(n^2)

(4)

    i=1;k=0;
    while(i<=n-1){
        k+=10*i;
        i++;
     }

//循环了n-1≈n次，所以是O(n)    

(5)

 for(i=1;i<=n;i++)
             for(j=1;j<=i;j++)
                 for(k=1;k<=j;k++)
                       x=x+1;

//循环了(1^2+2^2+3^2+...+n^2)=n(n+1)(2n+1)/6(这个公式要记住哦)≈(n^3)/3，不考虑系数，自然是O(n^3)

需要注意的是，在时间复杂度中，log(2,n)(以2为底)与lg(n)(以10为底)是等价的，因为对数换底公式：

log(a,b)=log(c,b)/log(c,a)

所以，log(2,n)=lgn/lg2，忽略掉系数，二者当然是等价的

在各种不同算法中，若算法中语句执行次数为一个常数，则时间复杂度为O(1)，譬如简单的求和，代码如下，其频度为3，O(1)

int a,b;  //频度为2
    printf("%d",a+b);  //频度为1  
    return 0;    

 　　

实践出真知，下面放一些更难的例题，帮助理解与计算时间复杂度

　　　

例一：下面是求50以内的奇数和的代码，求时间复杂度

 

（例 1.1）

 

 

（例 1.2）

    注意：其中的 floor() 和 ceil() 分别是向下取整和向上取整

 

 

例二：

 

while(n!=0)
{
    n/=10;  
}

　　

时间复杂度是O(lgn)

    解析：设规模为n,运行时间为T(n)。

            若n有五位数，则语句执行五次。

            设变量N==位数，则有当n有N位数时，语句执行N次。得N^10=n.

            则lgn=N。此时运行时间与问题规模的关系为 T(n) = c*N = c*lgn (c是常数) 

            所以时间复杂度为 O(lgn)

 

 

 

例三：

　

while(n!=0)
{
    n=n/2;
}

　　

    时间复杂度O(lgn)

    解析：

                设n=2^m,则循环执行了m+1次，m=1+log₂n=1 + lg(n)/lg(2)，因此频度为 1+lg(n)/lg(2)，运行时间 T(n) = 1 + lg(n) / lg(2)

                时间复杂度为 O(lgn)

 

例四：

void func(int n)
{ 
    int i=0,s=0;
    while(s<n)
    { 
        i++;
        s=s+i;
    }
}    

　　时间复杂度O(n^(1/2))

　　解析：　　　　

　　测试样例： n = 3，5，9，...n^2 ，可得频度 N = 2，3，4，...n^(1/2) （近似计算）

　　则运行时间 T(n) = c*(n^(1/2)) + c2 (c, c2为常数)，可得时间复杂度 O(n^(1/2))
　

　 

例五：　

　　x=91; y=100;
　　while(y>0)
　　{
           if(x>100)
　　    {
                x=x-10;
                y--;
            }
　　    else x++;
　　}                    

　　这题易错当为线性阶O(n)，我自己就犯了循环就是常数阶的错误，其实这是常数阶O(1)

 

 

常见算法的时间复杂度

---