第二届蓝桥杯省赛---夺冠概率

1. 夺冠概率

   足球比赛具有一定程度的偶然性，弱队也有战胜强队的可能。
   假设有甲、乙、丙、丁四个球队。根据他们过去比赛的成绩，得出每个队与另一个队对阵时取胜的概率表:

       甲 乙 丙 丁
   甲 - 0.1 0.3 0.5
   乙 0.9 - 0.7 0.4
   丙 0.7 0.3 - 0.2
   丁 0.5 0.6 0.8 -

   数据含义：甲对乙的取胜概率为0.1，丙对乙的胜率为0.3，...
   现在要举行一次锦标赛。双方抽签，分两个组比，获胜的两个队再争夺冠军。（参见【1.jpg】）

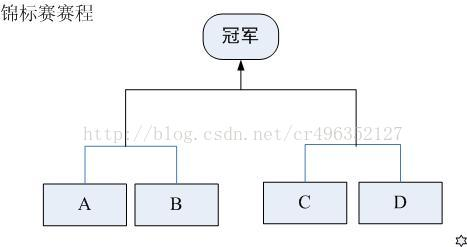
请你进行10万次模拟，计算出甲队夺冠的概率。

思路：题目给出了甲乙丙丁相互之间竞争取胜的各自的概率。现在要求模拟10万次比赛，求出甲队夺冠的概率，甲获胜比赛安排的类型是有限的。如下图：#

分析：一共有这三种情况，三种情况甲得冠的概率可以分别求出来，这三种概率相加就是甲得冠的理论概率（这个值是恒定的，因为这三种情况出现的概率都是1/3），

但是题目让模拟十万次，所以每一次的概率是不相同的，非常接近1/3，我们可以使用rand()函数随机获取0~2这三个数，用来体现着三种情况的随机性，十万次的概率相加，

用总和除以十万就是答案。。。

#include<iostream>
#include<cstdio>
#include<ctime>
#include<cstring>
using namespace std;

const int maxn = 1e5;
double t[3];

int main(){
    /*三种情况的概率*/
    t[0] = 0.1*0.8*0.5+0.1*0.2*0.3;
    t[1] = 0.3*0.6*0.5+0.3*.4*0.2;
    t[2] = 0.5*0.7*0.1+0.5*0.3*0.3;
    double sum=0;
    srand(time(NULL));
    for( int i=0; i<maxn; i++ ){
        sum+=t[rand()%3];
    }
    printf("%f
",sum/maxn);
    return 0;
}