题目
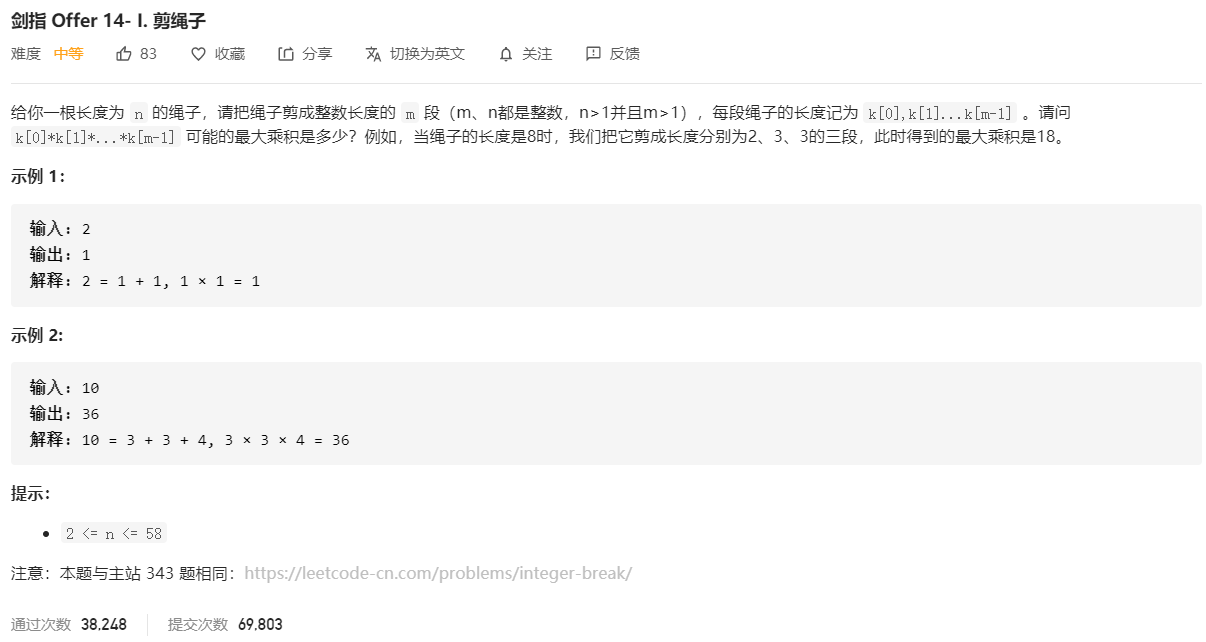
剑指 Offer 14- I. 剪绳子
我的思路
这也是个动态规划的问题,并且其中有套娃的思想
长度为n的绳子若被分成m段,长度依次为k1,...km时乘积最大
那么其中暗含了一个条件,(ki与kj属于k1...km)ki+kj绳长的绳子被分成ki和kj两段时乘积最大的。证明:如果存在比它还大的分割方法那么原长度为n绳子也有乘积更大的分割方法。反过来,长度为n的绳子在分割时一定选取的是多段子绳子的最优分割方法,否则不是乘积最大。
那么用一个数组L[],L[n]存储长度为n的绳子的最大乘积。
状态转移公式L[i+1]=max{L[t]+L[i+1-t]}, 0<=t<=(i+1)/2
更简单的思路,当绳子长度小于等于3时,因为必须分段,n=2时,result=1,n=3时,result=2
当绳子长度大于3时,一定是由2或3的小段组成的并且,长度为3的小段尽量多(因为2*2*2<3*3)。
所以大于3时,n/3=k,如果mod3=1,那么3^(k-1)*2*2;如果mod3=2,那么3^(k)*2;如果mod3=0,那么3^k;
我的实现
class Solution { public: int cuttingRope(int n) { if(n==2) return 1; else if(n==3) return 2; else{ int m = n%3; int k = n/3; if(m==0){ return pow(3,k); } else if(m==1){ return pow(3,k-1)*4; } else { return pow(3,k)*2; } } } }; /* 这也是个动态规划的问题,并且其中有套娃的思想 长度为n的绳子若被分成m段,长度依次为k1,...km时乘积最大 那么其中暗含了一个条件,(ki与kj属于k1...km)ki+kj绳长的绳子被分成ki和kj两段时乘积最大的。证明:如果存在比它还大的分割方法那么原长度为n绳子也有乘积更大的分割方法。反过来,长度为n的绳子在分割时一定选取的是多段子绳子的最优分割方法,否则不是乘积最大。 那么用一个数组L[],L[n]存储长度为n的绳子的最大乘积。 状态转移公式L[i+1]=max{L[t]+L[i+1-t]}, 0<=t<=(i+1)/2 更简单的思路,当绳子长度小于等于3时,因为必须分段,n=2时,result=1,n=3时,result=2 当绳子长度大于3时,一定是由2或3的小段组成的并且,长度为3的小段尽量多(因为2*2*2<3*3)。 所以大于3时,n/3=k,如果mod3=1,那么3^(k-1)*2*2;如果mod3=2,那么3^(k)*2;如果mod3=0,那么3^k; */