论文信息
论文标题:Graph Auto-Encoder via Neighborhood Wasserstein Reconstruction
论文作者:Shaked Brody, Uri Alon, Eran Yahav
论文来源:2022,ICLR
论文地址:download
论文代码:download
1 Abstract
提出了一种新的图自编码器,其中 Encoder 为普通的 GAE,而 Decoder 实现了特征重建、度重建,以及一种基于 2-Wasserstein distance 的邻居重建。
2 Introduction
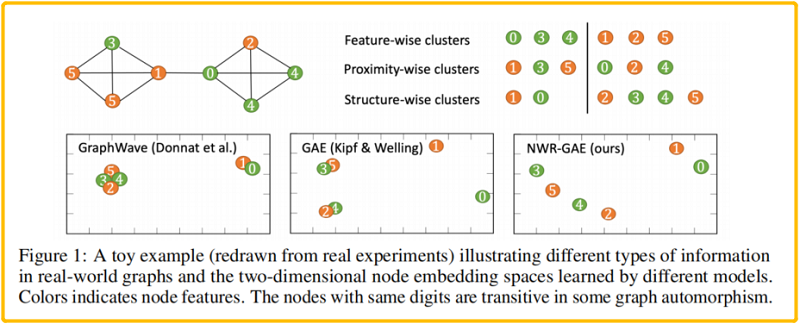
两种典型的 GAE :
-
- GAE(Kipf & Welling, 2016)使用简单的重建链接结构,导致无法区分像 (2, 4) 和 (3, 5)这样的点;
- GraphWave (Donnat et al., 2018) 面向结构的嵌入模型不考虑节点特征和空间接近度,无法区分像 (0, 1), (2, 4) 和 (3,5) 的节点对;
本文提出的 新框架为 Neighborhood Wasserstein Reconstruction Graph Auto-Encoder (NWR-GAE),将重构损失分解为三个部分,即 节点度、邻居表示分布和节点特征。
其中最重要的是重建邻居分布,由于在 $\text{k-hop}$ 消息传递后,在节点 $v$ 的表示中编码的信息来源本质上来自于 $v$ 的 $k-hop$ 邻域(Fig.2)。因此,节点 $v$ 的良好表示应该捕获其 $k$ 跳邻域中所有节点的特征信息,这与下游任务是无关的。

考虑两个分布之间的距离:当两个分布有非重叠的部分时,$f$ 散度家族存在非连续的问题。
Suppose we have two probability distributions, $P$ and $Q$ :
$\forall(x, y) \in P, x=0 \text { and } y \sim U(0,1) \forall(x, y) \in Q, x=\theta, 0 \leq \theta \leq 1 \text { and } y \sim U(0,1)$
When $\theta \neq 0$ :
$D_{K L}(P \| Q) =\sum\limits _{x=0, y \sim U(0,1)} 1 \cdot \log \frac{1}{0}=+\infty$
$D_{K L}(Q \| P) =\sum\limits_{x=0, y \sim U(0,1)} 1 \cdot \log \frac{1}{0}=+\infty$
$D_{J S}(P, Q) =\frac{1}{2}\left(\sum\limits_{x=0, y \sim U(0,1)} 1 \cdot \log \frac{1}{1 / 2}+\sum\limits_{x=0, y \sim U(0,1)} 1 \cdot \log \frac{1}{1 / 2}\right)=\log 2$
$W(P, Q) =|\theta| $
But when $\theta = 0$, two distributions are fully overlapped:
$D_{K L}(P \| Q) =D_{K L}(Q \| P)=D_{J S}(P, Q)=0$
$W(P, Q) =0=|\theta|$
可以使用 最优传输 OT 的 2-Wasserstein distance 衡量两个分布之间的距离,在这里,给出一个基于 2-Wasserstein distance 的常用的 OT 损失:
Definition 2.1. Let $\mathcal{P}$, $\mathcal{Q}$ denote two probability distributions with finite second moment defined on $\mathcal{Z} \subseteq \mathbb{R}^{m}$ . The 2-Wasserstein distance between $\mathcal{P}$ and $\mathcal{Q}$ defined on $\mathcal{Z}$, $\mathcal{Z}^{\prime} \subseteq \mathbb{R}^{m}$ is the solution to the optimal mass transportation problem with $\ell_{2}$ transport cost (Villani, 2008):
$\mathcal{W}_{2}(\mathcal{P}, \mathcal{Q})=\left(\inf _{\gamma \in \Gamma(\mathcal{P}, \mathcal{Q})} \int_{\mathcal{Z} \times \mathcal{Z}^{\prime}}\left\|Z-Z^{\prime}\right\|_{2}^{2} d \gamma\left(Z, Z^{\prime}\right)\right)^{1 / 2}$
where $\Gamma(\mathcal{P}, \mathcal{Q})$ contains all joint distributions of $\left(Z, Z^{\prime}\right)$ with marginals $\mathcal{P}$ and $\mathcal{Q}$ respectively.
3 Methods
预先定义 :
-
- Encoder:$\phi$
- Decoder:$\psi$
Encoder 可以是任何基于消息传递的 GNNs,Decoder 可以分成三部分:$\psi=\left(\psi_{s}, \psi_{p}, \psi_{d}\right)$
3.1 Neighborhood peconstruction principle
本文只考虑 1-hop 邻域重建。用 $H^{(0)}$ 代表 $X$ 初始特征矩阵,对于每个节点 $v \in V$ 被 GNN Enocoder 编码后 ,其节点表示 $h_{v}^{(1)}$ 从 $h_{v}^{(0)}$ 及其邻居表示 $H_{\mathcal{N}_{v}}^{(0)}=\left\{h_{u}^{(0)} \mid u \in \mathcal{N}_{v}\right\}$ 。本文主要目的是重构来自 $h_{v}^{(0)}$ 和 $H_{\mathcal{N}_{v}}^{(0)}$ 的信息,因此有
$\begin{array} {l}\underset{\phi, \psi}{\text{min}} & \sum\limits _{v \in V} \mathcal{M}\left(\left(h_{v}^{(0)}, H_{\mathcal{N}_{v}}^{(0)}\right), \psi\left(h_{v}^{(1)}\right)\right)\\\text { s.t. } & h_{v}^{(1)}=\phi\left(h_{v}^{(0)}, H_{\mathcal{N}_{v}}^{(0)}\right), \forall v \in V\end{array} \quad\quad\quad(2)$
其中,$\mathcal{M}(\cdot, \cdot)$ 定义了重建损失,$M$ 可分为两部分,分别测量自 特征重建 和 邻域重建:
$\mathcal{M}\left(\left(h_{v}^{(0)}, H_{\mathcal{N}_{v}}^{(0)}\right), \psi\left(h_{v}^{(1)}\right)\right)=\mathcal{M}_{s}\left(h_{v}^{(0)}, \psi\left(h_{v}^{(1)}\right)\right)+\mathcal{M}_{n}\left(H_{\mathcal{N}_{v}}^{(0)}, \psi\left(h_{v}^{(1)}\right)\right)\quad\quad\quad(3)$
对于特征重建,及其特征重建损失函数$\mathcal{M}_{s}$ :
$\mathcal{M}_{s}\left(h_{v}^{(0)}, \psi\left(h_{v}^{(1)}\right)\right)=\left\|h_{v}^{(0)}-\psi_{s}\left(h_{v}^{(1)}\right)\right\|^{2}\quad\quad\quad(4)$
代码中:
feature_losses = self.feature_loss_func(h0, self.feature_decoder(gij))
其实 h0 代表原始特征矩阵 $X$,而 gij 是经过四层的 GCN encoder 得到的隐表示,然后使用一个 FNN 的 feature_decoder 将 gij 的维度映射成和 $X$ 一样大。
$\mathcal{M}_{n}$ 被分为度重建和 邻居重建,对于节点 $v$,邻域信息被表示为 i.i.d .的经验实现从 $\mathcal{P}_{v}^{(0)}$ 中采样 $d_{v}$ 元素,其中 $\mathcal{P}_{v}^{(0)} \triangleq \frac{1}{d_{v}} \sum\limits _{u \in \mathcal{N}_{v}} \delta_{h_{u}^{(0)}}$。具体来说,采用
$\mathcal{M}_{n}\left(H_{\mathcal{N}_{v}}^{(0)}, \psi\left(h_{v}^{(1)}\right)\right)=\left(d_{v}-\psi_{d}\left(h_{v}^{(1)}\right)\right)^{2}+\mathcal{W}_{2}^{2}\left(\mathcal{P}_{v}^{(0)}, \psi_{p}^{(1)}\left(h_{v}^{(1)}\right)\right)\quad\quad\quad(5)$
Generalizing to k-hop neighborhood reconstruction

本文期望 $h_{v}^{(k)}$ 直接重构 $H_{\mathcal{N}_{v}}^{(i)}$ $i<k-1$。具体来说,对于每个节点 $v \in V$,使用重构损失
$\begin{array}{l}&\mathcal{M}^{\prime}\left(\left(h_{v}^{(0)},\left\{H_{\mathcal{N}_{v}}^{(i)} \mid 0 \leq i \leq k-1\right\}\right), \psi\left(h_{v}^{(k)}\right)\right)=\mathcal{M}_{s}\left(h_{v}^{(0)}, \psi\left(h_{v}^{(k)}\right)\right)+\sum\limits_{i=0}^{k-1} \mathcal{M}_{n}\left(H_{\mathcal{N}_{v}}^{(i)}, \psi\left(h_{v}^{(k)}\right)\right) \\&=\lambda_{s}\left\|h_{v}^{(0)}-\psi_{s}\left(h_{v}^{(k)}\right)\right\|^{2}+\lambda_{d}\left(d_{v}-\psi_{d}\left(h_{v}^{(k)}\right)\right)^{2}+\sum\limits_{i=0}^{k-1} \mathcal{W}_{2}^{2}\left(\mathcal{P}_{v}^{(i)}, \psi_{p}^{(i)}\left(h_{v}^{(k)}\right)\right)\end{array}\quad(6)$
其中 $\psi_{s}$ 是解码初始特征,$\psi_{d}$ 是度解码,$\psi_{p}^{(i)}$,$0 \leq i \leq k-1$ 是解码 $i$ 层邻域表示分布 $\mathcal{P}_{v}^{(i)}\left(: \triangleq \frac{1}{d_{v}} \sum\limits _{u \in \mathcal{N}_{v}} \delta_{h_{u}^{(i)}}\right)$。$\lambda_{s}$ 和 $\lambda_{d}$ 为非负性超参数。因此,$k$ 跳邻域重建的全部目标是
$\begin{array}{l} \underset{\phi, \psi}{\text{min}}\quad \sum\limits _{v \in V} \mathcal{M}^{\prime}\left(\left(h_{v}^{(0)},\left\{H_{\mathcal{N}_{v}}^{(i-1)} \mid 1 \leq i \leq k\right\}\right), \psi\left(h_{v}^{(k)}\right)\right)\\ \text { s.t. }\quad H^{(i)}=\phi^{(i)}\left(H^{(i-1)}\right), \quad1 \leq i \leq k\end{array}\quad(7)$
其中,$\phi=\left\{\phi^{(i)} \mid 1 \leq i \leq k\right\}$ 包括 $k$ 个GNN层,$\mathcal{M}^{\prime}$ 在 $\text{Eq.6}$ 中定义。
3.2 Decoding distributions——Decoders $\psi_{p}^{(i)}, 0 \leq i \leq k-1$
Note :上述图说的其实是使用 第 $k$ 的节点 $v$ 的节点表示$h_{v}^{(k)}$重建邻域 $H_{\mathcal{N}_{v}}^{(k-1)}$。
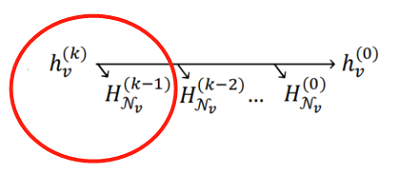
$\begin{array}{l}\psi_{p}^{(i)}\left(h_{v}^{(k)}\right)=\operatorname{FNN}_{p}^{(i)}(\xi),\quad \xi \sim \mathcal{N}\left(\mu_{v}, \Sigma_{v}\right)\\\text { where }\quad \mu_{v}=\operatorname{FNN}_{\mu}\left(h_{v}^{(k)}\right), \quad\Sigma_{v}=\operatorname{diag}\left(\exp \left(\operatorname{FNN}_{\sigma}\left(h_{v}^{(k)}\right)\right)\right)\end{array}\quad(8)$
上代码悟:
self.m = torch.distributions.Normal(torch.zeros(sample_size, hidden_dim),torch.ones(sample_size, hidden_dim))
self.mlp_mean = nn.Linear(hidden_dim, hidden_dim)
self.mlp_sigma = nn.Linear(hidden_dim, hidden_dim)
sampled_embeddings_list, mark_len_list = self.sample_neighbors(neighbor_indexes, neighbor_dict, to_layer) #从第 k-1 层采样节点的5个邻居节点,未满五个的使用 0 填充特征矩阵
for i, neighbor_embeddings1 in enumerate(sampled_embeddings_list):
# Generating h^k_v, reparameterization trick
index = neighbor_indexes[i]
mask_len1 = mark_len_list[i]
mean = from_layer[index].repeat(self.sample_size, 1) #[5,512] ,获取第 k 层的 节点 v 的表示
mean = self.mlp_mean(mean) #[5,512] ,线性变换
sigma = from_layer[index].repeat(self.sample_size, 1) #[5,512] ,获取第 k 层的 节点 v 的表示
sigma = self.mlp_sigma(sigma) #[5,512] ,线性变换
std_z = self.m.sample().to(device) # [5,512] ,每个元素为均值为0,标准差为1 的正态分布生成
var = mean + sigma.exp() * std_z # [5,512] 正态分布处理生成的邻居表示集合
nhij = FNN_generator(var, device) #[5,512] ,前馈神经网络线性变换
generated_neighbors = nhij
接着就去计算 节点 $v$ 的邻域 和生成的邻域之间的 2-Wasserstein distance ,这里的代码我没看懂,好难过啊。
3.3 Further discussion-Decoders $\psi_{s}$ 、$\psi_{d}$ and Encoder $\phi$
3.3.1 degree_decoder
重构节点度的解码器 $\psi_{d}$ 是一个 FNN+ReLU 激活函数,使其值非负。
$\psi_{d}(h_{v}^{(k)})=\exp (\mathrm{FNN}_{d}(h_{v}^{(k)}))\quad\quad\quad(9)$
度解码器代码:

self.degree_decoder = FNN(hidden_dim, hidden_dim, 1, 4)
# FNN
class FNN(nn.Module):
def __init__(self, in_features, hidden, out_features, layer_num):
super(FNN, self).__init__()
self.linear1 = MLP(layer_num, in_features, hidden, out_features)
self.linear2 = nn.Linear(out_features, out_features)
def forward(self, embedding):
x = self.linear1(embedding)
x = self.linear2(F.relu(x))
return x
def degree_decoding(self, node_embeddings):
degree_logits = F.relu(self.degree_decoder(node_embeddings))
return degree_logits
度重构采用的损失函数 MSE loss:
self.degree_loss_func = nn.MSELoss()
3.3.2 feature_decoder
重构初始特征 $h_{v}^{(0)}$ 的解码器 $\psi_{s}$ 是一个 FNN。
$\psi_{s}\left(h_{v}^{(k)}\right)=\mathrm{FNN}_{s}\left(h_{v}^{(k)}\right)\quad\quad\quad(9)$
特征解码器代码:

self.feature_decoder = FNN(hidden_dim, hidden_dim, in_dim, 3)
# FNN
class FNN(nn.Module):
def __init__(self, in_features, hidden, out_features, layer_num):
super(FNN, self).__init__()
self.linear1 = MLP(layer_num, in_features, hidden, out_features)
self.linear2 = nn.Linear(out_features, out_features)
def forward(self, embedding):
x = self.linear1(embedding)
x = self.linear2(F.relu(x))
return x
特征重构采用的损失函数 MSE loss:
self.feature_loss_func = nn.MSELoss()
3.3.3 Encoder
Encoder 可以为 GINConv、GraphConv、SAGEConv layer, 考虑到本实验堆叠了多层 GNNs layer,所以很容易造成过平滑,故,这里采用 PairNorm 缓解过平滑存在的问题。
$\begin{array}{l}\left\{h_{v}^{(0)} \mid v \in V\right\}=\text { pair-norm }\left(\left\{x_{v} W \mid v \in V\right\}\right) \\ \text {where } W \text { is a learnable parameter matrix. }\end{array}\quad\quad\quad(10)$
Encoder 代码:

if GNN_name == "GCN":
self.graphconv1 = GraphConv(in_dim, hidden_dim) #[1433,512]
self.graphconv2 = GraphConv(hidden_dim, hidden_dim) #[512,512]
self.graphconv3 = GraphConv(hidden_dim, hidden_dim) #[512,512]
self.graphconv4 = GraphConv(hidden_dim, hidden_dim) #[512,512]
self.norm = PairNorm(norm_mode, norm_scale)
def forward_encoder(self, g, h):
# K-layer Encoder
# Apply graph convolution and activation, pair-norm to avoid trivial solution
h0 = h
l1 = self.graphconv1(g, h0)
l1_norm = torch.relu(self.norm(l1))
l2 = self.graphconv2(g, l1_norm)
l2_norm = torch.relu(self.norm(l2))
l3 = self.graphconv3(g, l2)
l3_norm = torch.relu(l3)
l4 = self.graphconv4(g, l1_norm) # 5 layers
return l4, l3_norm, l2_norm, l1_norm, h0
class PairNorm(nn.Module):
...
def forward(self, x):
if self.mode == 'None':
return x
col_mean = x.mean(dim=0)
if self.mode == 'PN':
x = x - col_mean
rownorm_mean = (1e-6 + x.pow(2).sum(dim=1).mean()).sqrt()
x = self.scale * x / rownorm_mean
if self.mode == 'PN-SI':
x = x - col_mean
rownorm_individual = (1e-6 + x.pow(2).sum(dim=1, keepdim=True)).sqrt()
x = self.scale * x / rownorm_individual
if self.mode == 'PN-SCS':
rownorm_individual = (1e-6 + x.pow(2).sum(dim=1, keepdim=True)).sqrt()
x = self.scale * x / rownorm_individual - col_mean
return x
4 Experiments
我们设计实验来评估 NWR-GAE,重点关注以下研究问题:RQ1:与最先进的无监督图嵌入基线相比,NWR-GAE在基于结构角色的合成数据集上表现如何?RQ2:NWR-GAE及其消融如何与不同类型的真实世界图形数据集上的基线进行比较?RQ3:嵌入尺寸 $d$ 和采样尺寸 $q$ 等主要模型参数对NWR-GAE的影响是什么?
4.1 Experimental setup
4.1.1 Datasets
Synthetic datasets
4.1.2 Baselines
1) Random walk based (DeepWalk, node2vec)
2) Structural role based (RoleX, struc2vec, GraphWave)
3) Graph auto-encoder based (GAE, VGAE, ARGVA)
4) Contrastive learning based (DGI, GraphCL, MVGRL)
4.1.3 Evaluation metrics
- Homogeneity: conditional entropy of ground-truth among predicting clusters.
- Completeness: ratio of nodes with the same ground-truth labels assigned to the same cluster.
- Silhouette score: intra-cluster distance vs. inter-cluster distance.
4.2 Performance on synthetic datasets(RQ1)

4.3 Performance on real-world datasets(RQ2)
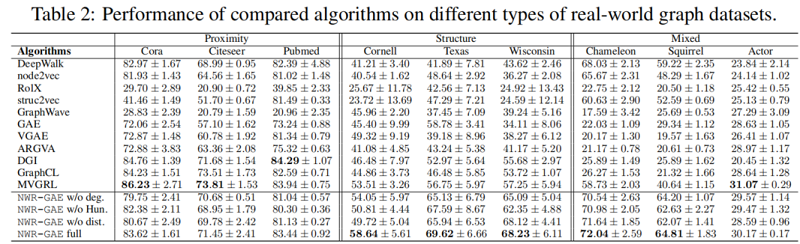
4.4 In-depth analysis of NWR-GAE
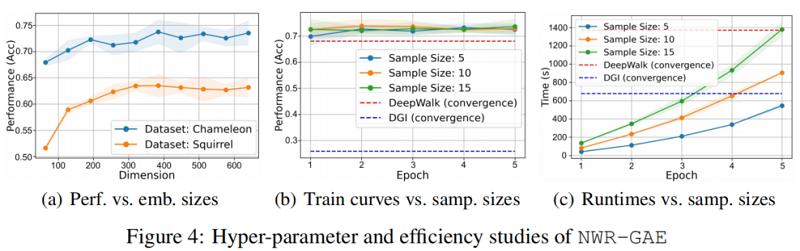
5 Conclusion
在这项工作中,我们解决了现有的无监督图表示方法的局限性,并提出了第一个能够正确地捕获图中节点的接近性、结构和特征信息的模型,并在低维嵌入空间中对其进行区分编码的模型。该模型在合成和真实基准数据集上进行了广泛的测试,结果有力地支持了其声称的优势。由于它是通用的,有效的,而且在概念上也很容易理解,我们相信它有潜力作为无监督图表示学习的实际方法。在未来,它将有望看到其在不同领域的应用研究,以及仔细分析其鲁棒性和隐私性等潜在问题。

