论文信息
论文标题:GCC: Graph Contrastive Coding for Graph Neural Network Pre-Training
论文作者:Jiezhong Qiu, Qibin Chen, Yuxiao Dong, Jing Zhang, Hongxia Yang, Ming Ding, Kuansan Wang, Jie Tang
论文来源:2020, KDD
论文地址:download
论文代码:download
1 Introduction
本文的预训练任务:子图实例判别(subgraph instance discrimination)。对于每个顶点,将其 r-ego networks 作为采样子图实例,GCC 的目的是区分从特定顶点采样的子图和从其他顶点采样的子图。
2 Related work
接下来介绍几种顶点相似性:
有边相连的节点被认为是相似的,邻居相似性方法有:
-
- Jaccard similarity (counting common neighbors)
- RWR similarity [36]
- SimRank [21]
Structural similarity
结构相似性的基本假设是,具有相似局部结构的顶点被认为是相似的。
第一种基于领域知识:
-
- vertex degree
- structural diversity [51]
- structural hole [7]
- k-core [2]
- motif [5, 32]
第二种基于谱图理论。
利用图数据属性,进一步度量相似性。
3 Method
Figure 2 展示了GCC的 pre-training 和 fine-tuning 阶段的概述。
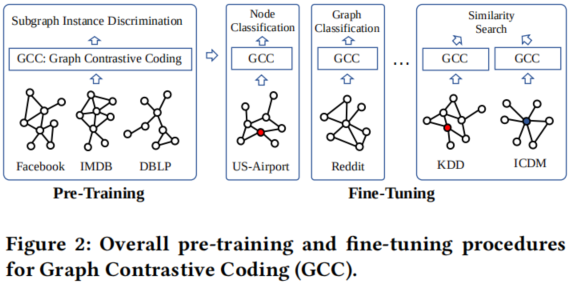
3.1 The GNN Pre-Training Problem
GNN 的训练目标是学习一个函数 $f$,将节点映射到一个低维的特征向量,具有以下两个属性:
-
- 首先,structural similarity,具有相似拓扑结构的节点在向量空间种映射相近;
- 其次,transferability,对于图中不可见的节点任然可以预测;
3.2 GCC Pre-Training
pre-training task 将其他子图实例视为自己的不同类,并学习区分这些实例。
${\large \mathcal{L}=-\log \frac{\exp \left(\boldsymbol{q}^{\top} \boldsymbol{k}_{+} / \tau\right)}{\sum\limits_{i=0}^{K} \exp \left(\boldsymbol{q}^{\top} \boldsymbol{k}_{i} / \tau\right)}} $
其中,$\tau$ 为温度超参数。$f_{q}$ 和 $f_{k}$ 是两个 GNN encoder ,将 query $x^{q}$ 和 keys $x^{k}$ 编码为 $d$ 维表示,用 $\boldsymbol{q}=f_{q}\left(x^{q}\right)$ 和 $\boldsymbol{k}=f_{k}\left(x^{k}\right)$ 表示。
Definition 3.1. A r-ego network. Let $G=(V, E)$ be a graph, where $V$ denotes the set of vertices and $E \subseteq V \times V$ denotes the set of edges . For a vertex $v$ , its r -neighbors are defined as $S_{v}=\{u : d(u, v) \leq r\}$ where $d(u, v)$ is the shortest path distance between $u$ and $v$ in the graph $G$ . The r -ego network of vertex $v$ , denoted by $G_{v}$ , is the sub-graph induced by $S_{v}$ .
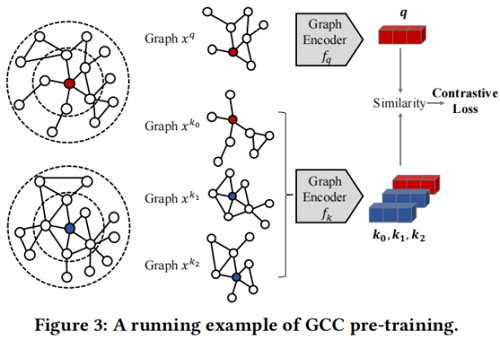
Q2: Define (dis)similar instances
在GCC中,将相同节点的 r-ego 网络作为一个相似的实例对,负样本通过图抽样生成。
GCC 的图采样遵循以下三个步骤:
-
- Random walk with restart。从顶点 $v$ 开始在 $G$ 上随机游走。该游走以与边权值成正比的概率迭代地移动到它的邻域。此外,在每一步中,游走有一定概率返回到起始顶点 $v$。
- Subgraph induction。根据上述游走路径获得顶点 $v$ 的顶点子集,用 $\widetilde{S}_{v}$ 表示。然后,用 $\widetilde{S}_{v}$ 生成诱导子图 $\widetilde{G}_{v}$ (ISRW 方法)。
- Anonymization。将上述采样的图节点重新打上标记 $\left\{1,2, \cdots,\left|\widetilde{S}_{v}\right|\right\}$ ,即将采样图的 $\widetilde{G}_{v}$ 匿名化。
重复上述过程两次来创建两个数据增强,形成一个正实例对 $\left(x^{q}, x^{k_{+}}\right)$。如果两个子图从不同的 r-ego networks 中获得,将它们视为一个具有 $k \neq k_{+}$ 的不同实例对 $\left(x^{q}, x^{k}\right)$。
回想一下,我们关注于结构表示预训练,而大多数GNN模型需要顶点特征/属性作为输入。为了弥合差距,我们利用每个采样子图的图结构来初始化顶点特征。具体来说,我们将广义位置嵌入定义如下:
Definition 3.2. Generalized positional embedding.For each subgraph, its generalized positional embedding is defined to be the top eigenvectors of its normalized graph Laplacian. Formally, suppose one subgraph has adjacency matrix $A$ and degree matrix $D$ , we conduct eigen-decomposition on its normalized graph Laplacian s.t. $\boldsymbol{I}-\boldsymbol{D}^{-1 / 2} \boldsymbol{A} D^{-1 / 2}=\boldsymbol{U} \boldsymbol{\Lambda} \boldsymbol{U}^{\top}$ , where the top eigenvectors in $\boldsymbol{U}$ are defined as generalized positional embedding.
FACT. The Laplacian of path graph has eigenvectors: $\boldsymbol{u}_{k}(i)= \cos (\pi k i / n-\pi k / 2 n)$ , for $1 \leq k \leq n, 1 \leq i \leq n$ . Here $n$ is the number of vertices in the path graph, and $\boldsymbol{u}_{k}(i)$ is the entry at $i-th$ row and $k-th$ column of $\boldsymbol{U}$ , i.e., $\boldsymbol{U}=\left[\begin{array}{lll}\boldsymbol{u}_{1} & \cdots & \boldsymbol{u}_{n}\end{array}\right]$ .
以上事实表明,在序列模型中的位置嵌入可以看作是路径图的拉普拉斯特征向量。这激发了我们将位置嵌入从路径图推广到任意图。使用标准化图拉普拉斯图而非非标准化图的原因是路径图是一个正则图(即常度),而现实世界的图通常是不规则的,有倾斜的度分布。除了广义位置嵌入外,我们还添加了顶点度[59]的独热编码和自我顶点的二进制指标作为顶点特征。在由图编码器编码后,最终的 $d$ 维输出向量然后用它们的 L2-Norm 进行归一化。
MoCo 旨在增加字典的大小,而不需要额外的反向传播成本。具体地说,MoCo 维护了来自之前小批次的样本队列。在优化过程中,MoCo 只通过反向传播来更新 $f_{q}$ 的参数(用 $\theta_{q}$ 表示)。$f_{k}$ 的参数(用 $\theta_{k}$ 表示)没有通过梯度下降进行更新。[17]等人为 $\theta_{k}$ 提出了一个基于动量的更新规则。形式上,MoCo 由 $\theta_{k} \leftarrow m \theta_{k}+(1-m) \theta_{q}$ 更新 $\theta_{k}$,其中 $m \in[0,1)$ 是一个动量超参数。上述动量更新规则在 $\theta_{q}$ 中逐步将更新传播到 $\theta_{k}$,使 $\theta_{k}$ 平稳、一致地发展。综上所述,MoCo以牺牲字典一致性为代价实现了更大的字典规模,即字典中的密钥表示由一个平滑变化的密钥编码器进行编码。
3.3 GCC Fine-Tuning
图学习中的下游任务通常可分为图级和节点级两类,其目标分别是预测图级或节点的标签。对于图级任务,输入图本身可以由 GCC 进行编码,以实现表示。对于节点级的任务,节点表示可以通过编码其 r-ego 网络(或从其 r-ego 网络增强的子图)来定义。
GCC为下游任务提供了两种微调策略——freezing mode 和 fine-tuning mode。
-
- 在 freezing mode 下,冻结预先训练的图编码器 $f_{q}$ 的参数,并将其作为静态特征提取器,然后在提取的特征之上训练针对特定下游任务的分类器。
- 在 fine-tuning mode 下,将用预先训练好的参数初始化的图编码器 $f_{q}$ 与分类器一起对下游任务进行端到端训练。
GCC作为一种图算法,属于局部算法类别,由于GCC通过基于随机游走(大规模)网络的图采样方法来探索局部结构,因此GCC只涉及对输入(大规模)网络的局部探索。这种特性使GCC能够扩展到大规模的图形学习任务,并对分布式计算设置非常友好。
4 Experiments

节点分类

图分类
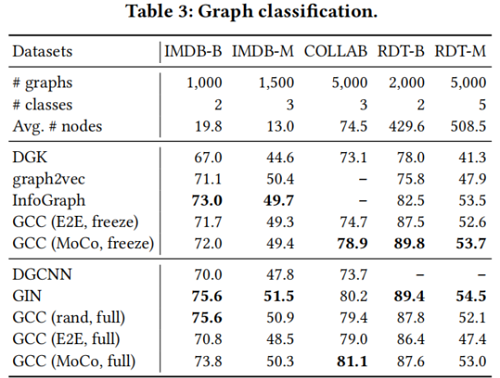
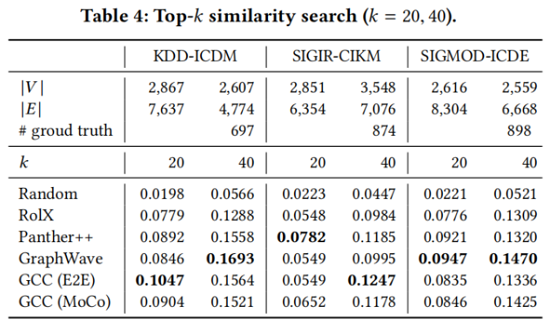
5 Conclusion
在本研究中,我们研究了图神经网络的预训练,目的是表征和转移社会和信息网络中的结构表征。我们提出了图对比编码(GCC),这是一个基于图的对比学习框架,用于从多个图数据集。预先训练的图神经网络在10个图数据集上的三个图学习任务中实现了与监督训练的从头开始的竞争性能。在未来,我们计划在更多样化的图形数据集上基准测试更多的图形学习任务,比如蛋白质-蛋白质关联网络。