题目链接:CF 706D
字典树水题,只是最近在膜可持久化字典树,拿这道题当模版写了一下,感觉跟主席树非常像,毕竟都是可持久化的思想,新建节点信息代替更改节点信息,写法也简单明了如果会主席树的话代码是不难理解的,只是最后返回的值是异或过的值,因为一个节点不再是模拟地去初始化、连接到链表尾,而是直接把节点的位置拿来标记为已使用,把信息复制到对应节点上去,因此需要一个变量cnt来记录这条路径有没有被覆盖过或者说有没有被使用过,有的话说明这条路到底是存在一个数,即用普通字典树的话来说就是这个点不为NULL,可以往下走。滋瓷范围内的Xor最大值的贪心查询
代码:
#include <bits/stdc++.h>
using namespace std;
const int N=200010;
struct Trie
{
int nxt[2];
int cnt;
};
Trie L[N*34];
int tot;
int root[N];
void init()
{
memset(L,0,sizeof(L));
tot=0;
}
void update(int &cur,int ori,int step,int n,int v)
{
cur=++tot;
L[cur]=L[ori];
L[cur].cnt+=v;
if(step<0)
return ;
int t=(n>>step)&1;
update(L[cur].nxt[t],L[ori].nxt[t],step-1,n,v);
}
int Find(int S,int E,int step,int n)
{
if(step<0)
return 0;
int t=(n>>step)&1;
if(L[L[E].nxt[t^1]].cnt-L[L[S].nxt[t^1]].cnt>0)
return (1<<step)+Find(L[S].nxt[t^1],L[E].nxt[t^1],step-1,n);
else
return Find(L[S].nxt[t],L[E].nxt[t],step-1,n);
}
int main(void)
{
int n,x,i;
char ops[3];
while (~scanf("%d",&n))
{
init();
update(root[1],root[0],31,0,1);
int op=1;
int sz=0;
for (i=1; i<=n; ++i)
{
scanf("%s",ops);
if(ops[0]=='+')
{
++sz;
++op;
scanf("%d",&x);
update(root[op],root[op-1],31,x,1);
}
else if(ops[0]=='-')
{
--sz;
++op;
scanf("%d",&x);
update(root[op],root[op-1],31,x,-1);
}
else
{
scanf("%d",&x);
if(!sz)
{
printf("%d
",x);
continue;
}
printf("%d
",Find(root[0],root[op],31,x));
}
}
}
}
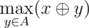 , i.e. the maximum value of bitwise exclusive OR (also know as XOR) of integer
, i.e. the maximum value of bitwise exclusive OR (also know as XOR) of integer 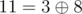 — maximum among integers
— maximum among integers 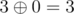 ,
, 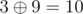 ,
, 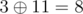 ,
, 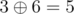 and
and 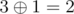 .
.