

思路:用递归来做感觉比动态规划简单,题目让我们判断s1和s2是否是scramble string,则s1上(从左起计数)有一个长度为 i 的分割点将s1分为s1_l 和 s1_r 两段 分别与 s2的(从左起计数一个长度为i的) s2_l 和 s2_r 互为 scramble string;或者与 s2的(从右起计数一个长度为i的)s2.substr(s-i) 和 s2.substr(0, s-i) 互为 scramble string 。
1)C++ 中的 substr(pos, len) 表示从 索引为pos开始的子字符串,截取长度为len的子串,即子串的索引为[pos, pos+len) 注意是左闭右开区间; substr(pos) 表示从索引pos开始到字符串末尾的子字符串,即 [pos, size ) size为字符串长度,注意是左闭右开区间。
2)sort() 可以按字典序排列 string 类型的字符串。
3)== 可以用来判断两个字符串是否相同。
class Solution { public: bool isScramble(string s1, string s2) { int s = s2.size(); if(s1.size()!=s2.size()) return false; if(s1==s2) return true; string str1 = s1, str2 = s2; sort(str1.begin(), str1.end()); sort(str2.begin(), str2.end()); if(str1 != str2) return false; for(int i=1; i<s1.size(); ++i){ string st1_l = s1.substr(0, i), st1_r = s1.substr(i); string st2_l = s2.substr(0, i), st2_r = s2.substr(i); if((isScramble(st1_l, st2_l) && isScramble(st1_r, st2_r)) || ( isScramble(st1_l, s2.substr(s-i) ) && isScramble(st1_r, s2.substr(0, s-i) ) )) return true; } return false; } };
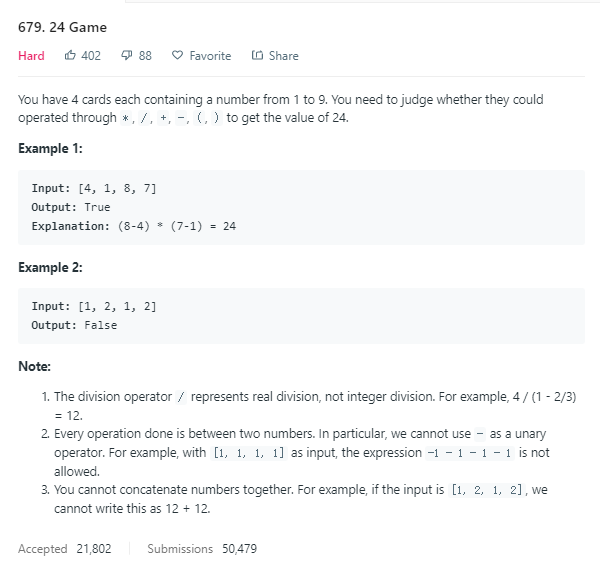
递归:注意 / 的意思是浮点数的除法,所以要先将int型的nums转化为 double 型的 arr;每次选两个索引位置不相同的元素,进行加减乘除操作,并将结果放入数组中,然后递归求解,直到数组最后只剩下一个元素,若这个元素值为24,则返回true。最后若两层遍历结束后都没有找到最后的结果为24,则返回false。
class Solution { public: bool judgePoint24(vector<int>& nums) { vector<double> arr(nums.begin(), nums.end()); return helper(arr); } bool helper(vector<double>& arr){ int size = arr.size(); if(size == 1 ) return (abs(arr[0] - 24) < 1e-6); for(int i=0; i<size; ++i){ for(int j=0; j<size; ++j){ if(i==j) continue; //不能取相同的元素 vector<double> new_arr; for(int k=0; k<size; ++k) if(k!=i && k!=j) new_arr.push_back(arr[k]); new_arr.push_back(-1); double a = arr[i], b = arr[j]; new_arr.back() = a+b; if (helper(new_arr)) return true; new_arr.back() = a-b; if (helper(new_arr)) return true; new_arr.back() = a*b; if (helper(new_arr)) return true; new_arr.back() = a/b; if (helper(new_arr)) return true; } } return false; } };

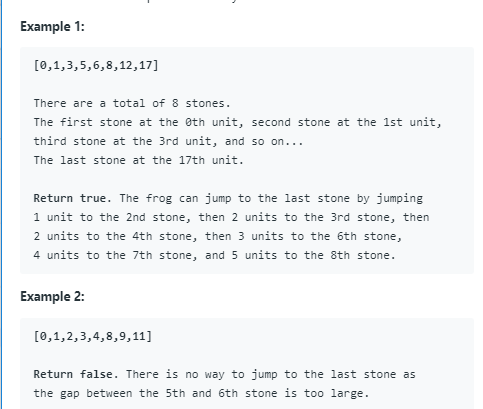
感觉这道题的题意有点难理解啊!而且难哭了 :(
1)青蛙初始在第一块石头上,假设一开始只能跳一个单位
2)若青蛙前一步跳了k个单位,则它的下一步只能是k-1, k, k+1 个单位。且只能往前跳不能往后退。
动态规划: 使用map,它的key 表示当前石头的位置pos,value 是一个包含 jumpsize的集合set,其中每个 jumpsize 代表可以通过大小为 jumpysize 大小的一跳到达当前位置。首先对map初始化,key 为所有石头的位置,除了位置 0 对应的 value 为包含一个值 0 的集合以外(dp[0] = 0 ),其余都初始化为空集。接下来,依次遍历每个位置上的石头。对于每个currentPosition,遍历 value 中每个 jumpsize,,对于每个 jumpsize,newjumpsize 分别为 jumpsize−1,jumpsize,jumpsize+1, 判断位置 currentPosition + newjumpsize 是否存在于 map 中。如果找到了,就在位置 currentPosition + newjumpsize 对应的 value 集合里新增 newjumpsize。重复这个过程直到结束。如果在结束的时候,最后一个位置对应的集合非空,那也就意味着我们可以到达终点,如果还是空集那就意味着不能到达终点。
class Solution { public: bool canCross(vector<int>& stones) { unordered_map<int, unordered_set<int>> dp; for (auto position : stones) dp[position] = unordered_set<int>(); dp[0].insert(0); for (auto position : stones) { for (auto k : dp[position]) { // k - 1 if (k - 1 > 0 && dp.find(position + k - 1) != dp.end()) dp[position + k - 1].insert(k - 1); // k if (dp.find(position + k) != dp.end()) dp[position + k].insert(k); // k + 1 if (dp.find(position + k + 1) != dp.end()) dp[position + k + 1].insert(k + 1); } } return !dp[stones.back()].empty(); } };