单源最短路径问题:给定一个带权有向图 G = (V, E), 其中每条边的权是一个实数.另外,还给定 V 中的一个顶点,称为源.现在要计算从源到其他所有各顶点的最短路径长度.这里的长度是指路上各边权之和.这个问题通常称为单源最短路径问题.
Dijkstra算法:
一:基本算法
将图 G 中所有的顶点 V 分成两个顶点集合 VA 和 VB.如果源点 S 到 u 的最短路径已经确定,则点 u 属于集合 VA ,否则属于集合 VB.最开始的时候 VA 只包含源点 S,其余的点属于 VB,算法结束时所有由源点 S 可达的点属于 VA ,由源点 S 不可达的点仍留在 VB 中.可以在求出最短路径长的同时记录最短路径,方法是距离终点的前一个点,这样只要倒着往回查就能确定整条最短路径.算法的适用范围是权值非负的图,即解决带有非负权值的图中的单源最短路径问题.
二:具体步骤
(1):首先初始化,将源点 S 到图中各点的直接距离当做初始值记录为 S 到各点的最短距离,如果不能直接到达,记为 INF, S 到 S 的距离为 0.
(2):在所有属于 VB 的点中找一个 S 到其路径长度最短的点 u, 将 u 从VB 中除去,加入到 VA 中,即当前求出的从 S 到 u 的路径为 S 到 u 的最短路径.
(3):由新确定的 u 点更新 S 到 VB 中每一点 v 的距离, 如果 S 到 u 的距离加上 u 到 v 的直接距离小于当前 S 到 v 的距离,表明新生成的最短路径的长度要比前面计算的更短,那么就更新这个距离,同时更新最短路径.
(4):重复(2),(3)步骤,直到VB 中已经没有剩余的点或者VB 中的点都不能由源点 S 到达为止.
三:伪代码
在这里, s 代表源, setA[] 记录点属于哪个集合: true 表示属于VA , false 表示属于VB ; map[][] 记录图的信息, map[u][v]为点 u 到点 v 的边的长度, 结果保存在 dist[]中,pre[]记录最短路径终点的前趋.
(1):初始化:源的距离 dist[s] 设为0,其他的点距离设为 map[s][i],即 dist[i] = map[s][i].setA[s]设为 true,其他各点的p[i] = false.
(2):循环 n - 1次:
a:在 VB 中的点中取一 s 到其距离最小的点 k, setA[k] = true. 如果所有的 k 都不可达,退出循环,算法结束.
b:对于每个与 k 相邻且在 VB 中的点 j,更新 s 到 j 的最短路径. 如果 dist[k] + map[k][j] < dist[j], 那么 dist[j] = dist[k] + map[k][j], 此时到点 j 的最短路径上, 终点 j 的前一个节点即为 k, 即 pre[j] = k.
四:以图为例
初始化图:

初始化数组:
dist 1 2 3 4 5 6
0 INF 10 INF 30 100
setA 1 2 3 4 5 6
1 0 0 0 0 0
第一步:
从 dist 数组中选择属于集合 B 且与 点“1” 距离最短的点,显然是点 “3”, 把点 “3” 加入集合 A.则改变后的图为:

然后选择与点 “3” 相邻的点且属于集合 B 的点,只有点 4,选择之后更新:
dist[4](INF) < dist[3](10) + map[3][4](50) 显然这里是成立的, 则dist[4] = dist[3] + map[3][4] = 60,更新后的数组为:
dist 1 2 3 4 5 6
0 INF 10 60 30 100
setA 1 2 3 4 5 6
1 0 1 0 0 0
第二步:
再次从 dist 数组中选择属于集合 B 且距离 源点 “1” 最短的点,可以看出这次拓展的点是点 “5”,把点 “5”加入集合A,图变为:

选择与点 “5” 相邻的点且属于集合 B 的点,这里有点 “4” 和点 “6”.则做比较更新:
点“4”: dist[4](60) < dist[5](30) + map[5][4](20) 这里是成立的,则dist[4] = dist[5](30) + map[5][4](20) = 50;
点“6”: dist[6] < dist[5](30) + map[5][6](60) 这也是成立的,则 dist[6] = dist[5] + map[5][6] = 90;
更新数组得:
dist 1 2 3 4 5 6
0 INF 10 50 30 90
setA 1 2 3 4 5 6
1 0 1 0 1 0
第三步:
再次选择符合条件的点,可知下一个待扩展点为点 “4”.
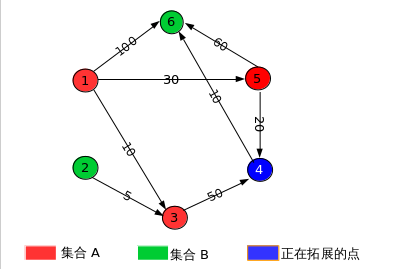
同样选择与点“4”相邻且属于集合B的点,可选点为 点 “6”.对点 “6”做更新:
dist[6](90) < dist[4](50) + map[4][6](10) 这里也是成立的,那么dist[6] = dist[4] + map[4][6] = 60. 更新后的数组为.
dist 1 2 3 4 5 6
0 INF 10 50 30 60
setA 1 2 3 4 5 6
1 0 1 1 1 0
第四步:
继续再集合B中选择距离源点最短的点,可得点 “6”.

由于此时已经没有和点 “6”相邻,且属于集合B的点了.那么把点 “6” 加入集合A继续下一步.
dist 1 2 3 4 5 6
0 INF 10 50 30 60
setA 1 2 3 4 5 6
1 0 1 1 1 1
第五步:
此时满足距离源点最短且属于集合B的点不存在,即剩下的属于集合B的点,已不可到达那么此时算法结束:

算法结束后,dist数组里保存的就是图中每点到源点的最短距离:
dist 1 2 3 4 5 6
0 INF 10 50 30 60
其中点 “2”为 不可到达.
五:代码
1 const int INF = INT_MAX; 2 const int MAXN =10000; 3 int mmap[MAXN + 3][MAXN + 3];//记录图的信息 4 int dist[MAXN + 3];//dist[i]表示点 i 到源点的最短距离 5 int pre[MAXN + 3];//记录前趋 记录最短路径 6 bool setA[MAXN + 3];//是否属于集合A,集合A代表着已经确定最短路径的点集 7 8 void Dijkstra(int n, int s) {// s 为源点 9 for(int i = 1; i <= n; i++) { //初始化 10 setA[i] = false; 11 if(i != s) { 12 dist[i] = mmap[s][i]; 13 pre[i] = s; 14 } 15 } 16 dist[s] = 0, setA[s] = true; 17 for(int i = 1; i <= n - 1; i++) {//求 s 到其他 n - 1个节点的最短路径 18 int minn = INF; 19 int k = 0; 20 for(int j = 1; j <= n; j++) { // 在属于集合 Vb 的点中取一点, 满足 s 到其的距离最小 21 if(!setA[j] && dist[j] < minn) { 22 minn = dist[j], k = j; 23 } 24 } 25 if(!k) return; // 没有点可以扩展,即剩余的点不可达,则结束算法 26 setA[k] = true; //将新找的点从集合 Vb 中除去, 加入集合 Va 27 for(int j = 1; j <= n; j++) { 28 //对于每个与 k 相邻 且属于 Vb 的点,更新 s 到 j 的最短路径 29 if(!setA[j] && mmap[k][j] != INF && dist[j] > dist[k] + mmap[k][j]) { 30 dist[j] = dist[k] + mmap[k][j]; 31 pre[j] = k; 32 } 33 } 34 } 35 }
参考文献:<<图论及应用>> <<数据结构>>