字符串
定义:
串(string)是由零个或多个字符组成的有限序列,又名叫字符串。
- 一般地,由n个字符串构成的串记作: S="a0a1......an-1"(n≥0),其中a_i(1≤i≤n)
- n是一个有限的数值
- 串一般记为S是串的名称,用双引号或单引号括起来的字符序列是串的值(引号不属于串的内容)。
- 可以是字母、数字或其他字符,i就是该字符在串中的位置。串中的字符数目n称为串的长度,n是一个有限的数值。
特征:
- 结构简单,(以二进制字符为例,仅 0,1两种字符构成)
- 规模庞大,
- 元素(字符)重复率高
子串
在对字符串S做处理时,经常需要取出其中某一连续的片段,称为S的子串(substring)
- 具体地,由串S中起始于位置i的连续k个字符组成的子串记作
substr(S,i,k) = "aiai+1...ai+k-1",0≤i 〈 n,0≤k - 前缀 prefix(S,k) = substr(S,0,k);
- 后缀 suffix(S,k) = substr(S,n-k,k)
- 空格串:只包含空格的串。
结论
- 空串是任何字符串的子串,也是任何字符串的前缀和后缀
- 任何字符串都是自己的子串,也是自己的前缀和后缀。此类子串,前缀和后缀分别称为平凡子串,平凡前缀,平凡后缀
- 字符串本身之外的所以非空子串,前缀,后缀,分别称为真子串,真前缀,真后缀
判定
一对字符串S="a0a1......an-1" 和 T="b0b1......bm-1",当且仅当二者长度相等(n=m),
且对应的字符分别相等(对任何0≤i 〈n,都有ai = bi)
模式匹配算法
朴素的模式匹配算法(BF(Brute-Force)算法)
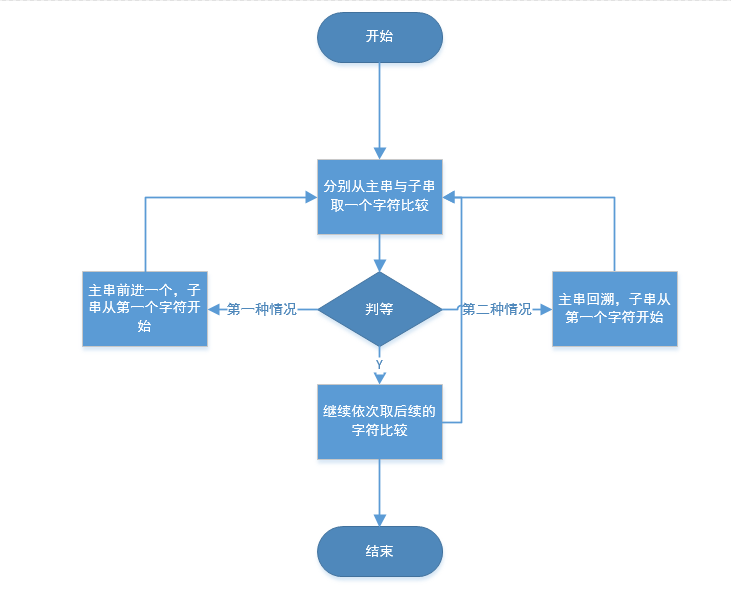
- 基本思想是:
- 从主串的第一个字符起与子串的第一个字符进行比较,若相等,则继续逐对字符进行后续的比较;
- 若不相等,则从主串第二个字符起与子串的第一个字符重新比较,以此类推,
直到子串中每个字符依次和主串中的一个连续的字符序列相等为止,此时称为匹配成功。 - 如果不能在主串中找到与子串相同的字符序列,则匹配失败。
- BF算法是最原始、最暴力的求解过程,但也是其他匹配算法的基础

public static void bruteForce(String s, String p) {
int index = -1;// 成功匹配的位置
int sLength = s.length();// 主串长度
int pLength = p.length();// 子串长度
if (sLength < pLength) {
System.out.println("Error.The main string is greater than the sub string length.");
return;
}
int i = 0;
int j = 0;
while (i < sLength && j < pLength) {
if (s.charAt(i) == p.charAt(j)) {// 判断对应位置的字符是否相等
i++;// 若相等,主串、子串继续依次比较
j++;
} else {// 若不相等
i = i - j + 1;// 主串回溯到上次开始匹配的下一个字符
j = 0;// 子串从头开始重新匹配
}
}
if (j >= pLength) {// 匹配成功
index = i - j;
System.out.println("Successful match,index is:" + index);
} else {// 匹配失败
System.out.println("Match failed.");
}
}
KMP
P模式匹配算法,是一个效率非常高的字符串匹配算法。其全称是Knuth–Morris–Pratt string searching algorithm
- 其核心思想就是主串不回溯,模式串尽量多地往右移动
- 即: N(P, j) = {t | prefix(prefix(P, j), t) = suffix(prefix(P, j), t), 0≤ t 〈 j } shift = j -t shift就是本次移动
地最大步长
构建next表
- 因为空串是任何非空串的真字串,真前缀,真后缀,故只要 j > 0,则必有 0 ∈ N(P, j)。
此时N(P, j) 必非空,从而保证“在其中取最大值”这一操作可行。反之。若j=0,则前缀prefix(P, j)
本身就是空串,它没有真子串,于是必有集合N(P, j) = φ。此种情况下,next[0] 该如何定义呢? - 按照串匹配算法的构思,倘若某轮迭代中第一对字符即失配,则应该将模式串P直接右移一位,然后从其首字符继续下一轮对比
就实际效果而言,这一处理方法完全等价于“令next[0] = -1”。 - 下面以模式串 "ABCDABD" 为例来详细说明是如何构建next表的
P = ABCDABD
j = 0, prefix(P, 0) = φ
next[0] = -1;//规定如此
P = ABCDABD
j = 1, prefix(P, 1) = A
真前缀: φ
真后缀: φ
next[1] = 0;
P = ABCDABD
j = 2, prefix(P, 2) = AB
真前缀: A
真后缀: B
next[2] = 0;
P = ABCDABD
j = 3, prefix(P, 3) = ABC
真前缀: A,AB
真后缀: BC,C
next[3] = 0;
P = ABCDABD
j = 4, prefix(P, 4) = ABCD
真前缀: A,AB,ABC
真后缀: BCD,CD,D
next[4] = 0;
P = ABCDABD
j = 5, prefix(P, 5) = ABCDA
真前缀: A,AB,ABC,ABCD
真后缀: BCDA,CDA,DA,A
next[5] = 1;
P = ABCDABD
j = 6, prefix(P, 6) = ABCDAB
真前缀: A,AB,ABC,ABCD,ABCDA
真后缀: BCDAB,CDAB,DAB,AB,B
next[6] = 2;
得出next表为:
[-1, 0, 0, 0, 0, 1, 2]
接下来就是代码实现:
//第一步构造next表
public static int[] buildNext(String p){
//构建next表就是查找真前缀 == 真后缀的最大长度,以获取模式串尽量多地往右移动
int[] N = new int[p.length()];
int m = p.length(),j = 0;//主串位置
int t = N[0] = -1;//字串位置
while(j < m -1){
if(t < 0 || p.charAt(j) == p.charAt(t)){
j++;t++;
N[j] = t;
}else{//失配
t = N[t];
}
}
return N;
}
//第二步利用next表尽量多地往右移动
public static void kmp(String s, String p) {
int[] next = buildNext(p);// 调用next(String p)方法
int index = -1;// 成功匹配的位置
int sLength = s.length();// 主串长度
int pLength = p.length();// 子串长度
if (sLength < pLength) {
System.out.println("Error.The main string is greater than the sub string length.");
return;
}
int i = 0;
int j = 0;
while (i < sLength && j < pLength) {
/*
* 如果j = -1, 或者当前字符匹配成功(即s.charAt(i) == p.charAt(j)), 都令i++,j++
* 这两个条件能否交换次序?
*/
if (j == -1 || s.charAt(i) == p.charAt(j)) {
i++;
j++;
} else {
/*
* 如果j != -1,且当前字符匹配失败, 则令 i 不变,j = next[j], next[j]即为j所对应的next值
*/
j = next[j];
}
}
if (j >= pLength) {// 匹配成功
index = i - j;
System.out.println("Successful match,index is:" + index);
} else {// 匹配失败
System.out.println("Match failed.");
}
}