01 分数规划
基本01分数规划问题
给定一个二元组 ((value_i,cost_i)) ,(value_i) 是选择此二元组获得的价值(非负),(cost_i) 是这个二元组的代价(非负),设 (x_i (x_i in {0, 1})) 表示第 (i) 个二元组选不选,最大化(最小化)下面柿子
[max(min)~r = frac{sum value_i * x_i}{sum cost_i * x_i} ]
下面以最大值为例(最小值也一个样)
构造一个函数
(f(r) = sum value_i * x_i - r * sum{cost_i * x_i})
对于如果 (x_i) 确定那么 (f(r)) 就成了 (f(r) = -kr + b) 的一条直线 (k, b) 都为常数
因为 (value_i) 和 (cost_i) 都非负,所以 (k, b > 0) ,所有直线都是一条斜率为负,纵截距为正的直线
画出来是这样的
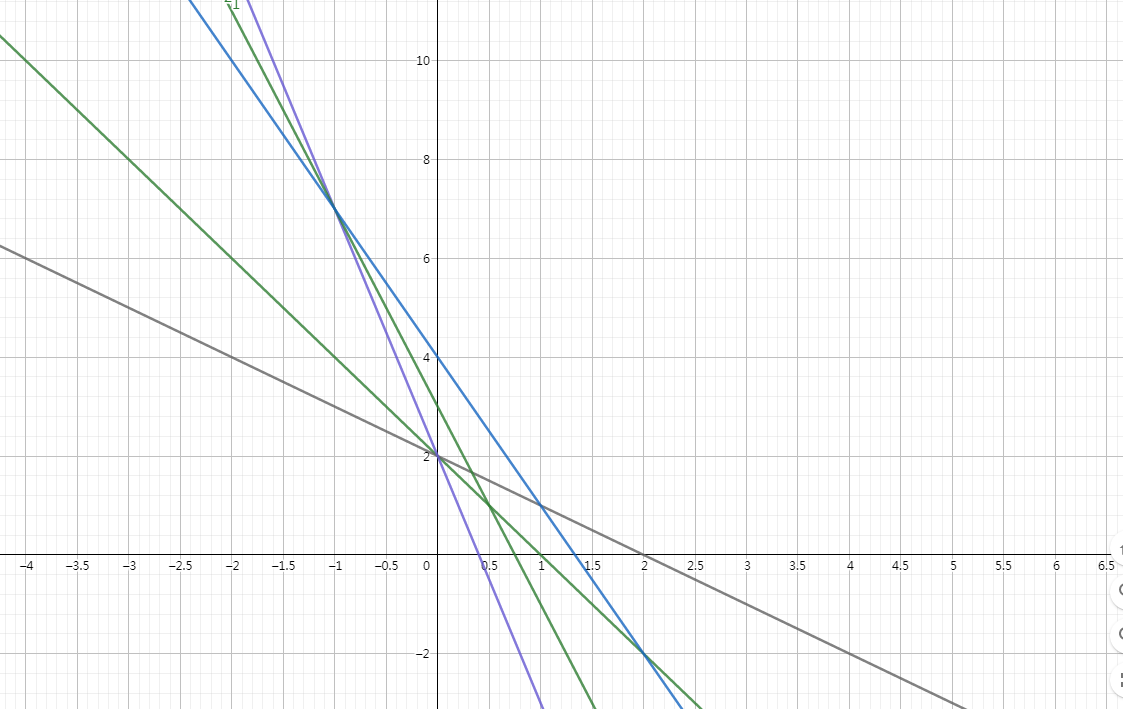
求最大的 (r) 就是求一条横截距最大的直线
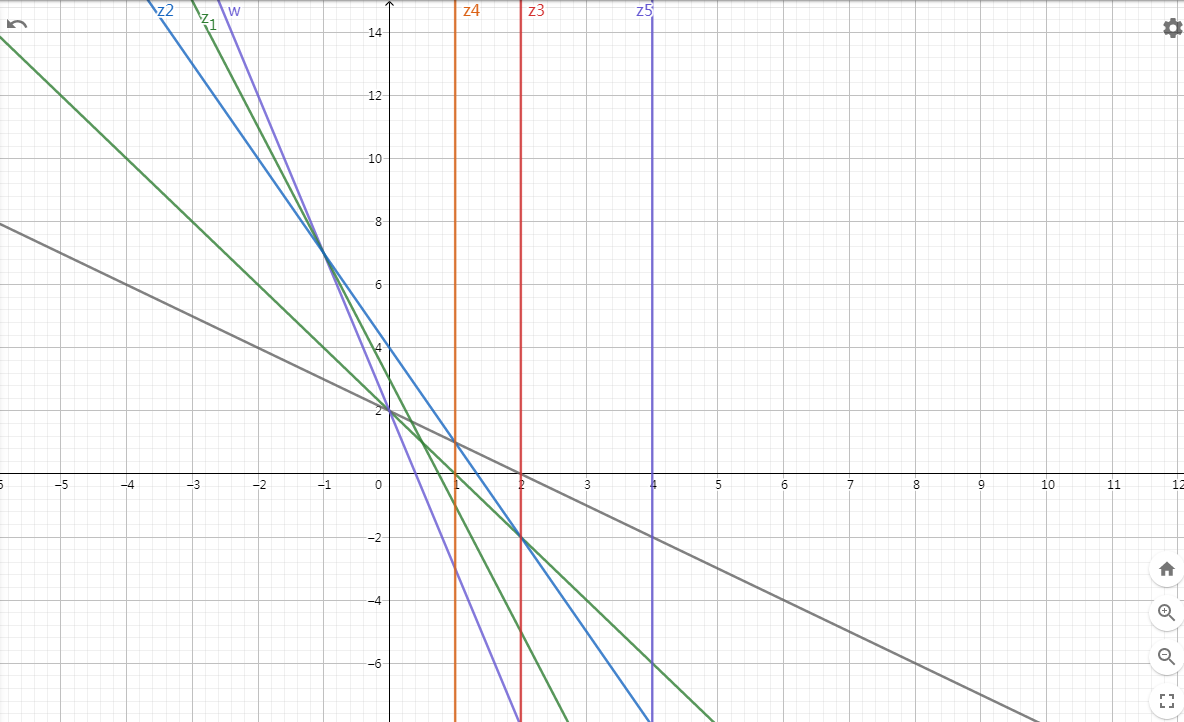
求一条垂直于 (y) 的线
- 如果存在直线与这条直线的交点纵坐标为正,则最优解在该直线右边
- 如果所有直线与这条直线的交点纵坐标为负,则最优解在该直线左边
- 如果一条直线与该直线交点纵坐标为 0,其余都为负,则该交点横坐标为最优解 (max_r)
具体实现
对 (r) 二分答案
-
(max(f(r)) > 0) ,(max_r > r) 二分右区间
-
(max(f(r)) < 0), (max_r < r) 二分左区间
-
(max(f(r)) = 0) ,(max_r = r) 统计答案
接下来就剩怎么求 (max(f(r))) 了
对上面的柿子稍微变一下形
(f(r) = sum (value_i - r * cost_i)*x_i)
对于前面的一坨如果知道了 (r) 可以直接求,然后现在就是找一组 (x_i) 使得 (f(r)) 最大,怎么求这一组 (x_i),要根据具体题目分析
最优比率环基本模型
luogu P2868 [USACO07DEC]Sightseeing Cows G
题目大意:
(N) 个点,(M) 条边的有向图,从中找出一个环,使得环上 $ P = frac{sum_{i =1}^{i leq n}F_i}{sum_{i = 1}^{i leq m}T_i}$ 最大
solution
根据上面所说,先把式子变形
$ sum_{i =1}^{i leq n}F_i - P * sum_{i = 1}^{i leq m}T_i = 0$
把柿子化成函数形式
$F(p) = sum_{i =1}^{i leq n}F_i - P * sum_{i = 1}^{i leq m}T_i $
和上面一样对 (P) 二分答案, 接着判断二分的 (P) 合不合法
也就是判断 $sum_{i =1}^{i leq n}F_i - P * sum_{i = 1}^{i leq m}T_i $ 与 0 的关系,那就要想办法求出 (F(p))
观察右边的柿子,其实不难发现它的本质就是找一个环,而判断与 (0) 的关系就是看在图中是否能找一个符合条件的正环
坑点:二分时的精度