《算法导论》读书笔记之第15章 动态规划—装配线调度

前言：动态规划的概念

　　动态规划（dynamic programming）是通过组合子问题的解而解决整个问题的。分治算法是指将问题划分为一些独立的子问题，递归的求解各个问题，然后合并子问题的解而得到原问题的解。例如归并排序，快速排序都是采用分治算法思想。本书在第二章介绍归并排序时，详细介绍了分治算法的操作步骤，详细的内容请参考：http://www.cnblogs.com/Anker/archive/2013/01/22/2871042.html。而动态规划与此不同，适用于子问题不是独立的情况，也就是说各个子问题包含有公共的子问题。如在这种情况下，用分治算法则会重复做不必要的工作。采用动态规划算法对每个子问题只求解一次，将其结果存放到一张表中，以供后面的子问题参考，从而避免每次遇到各个子问题时重新计算答案。

动态规划与分治法之间的区别：
（1）分治法是指将问题分成一些独立的子问题，递归的求解各子问题
（2）动态规划适用于这些子问题不是独立的情况，也就是各子问题包含公共子问题

　　动态规划通常用于最优化问题（此类问题一般有很多可行解，我们希望从这些解中找出一个具有最优（最大或最小）值的解）。动态规划算法的设计分为以下四个步骤：

（1）描述最优解的结构

（2）递归定义最优解的值

（3）按自低向上的方式计算最优解的值

（4）由计算出的结果构造一个最优解

　　动态规划最重要的就是要找出最优解的子结构。书中接下来列举4个问题，讲解如何利用动态规划方法来解决。动态规划的内容比较多，我计划每个问题都认真分析，写成日志。今天先来看第一个问题：装配线调度问题

2、问题描述

　　一个汽车公司在有2条装配线的工厂内生产汽车，每条装配线有n个装配站，不同装配线上对应的装配站执行的功能相同，但是每个站执行的时间是不同的。在装配汽车时，为了提高速度，可以在这两天装配线上的装配站中做出选择，即可以将部分完成的汽车在任何装配站上从一条装配线移到另一条装配线上。装配过程如下图所示：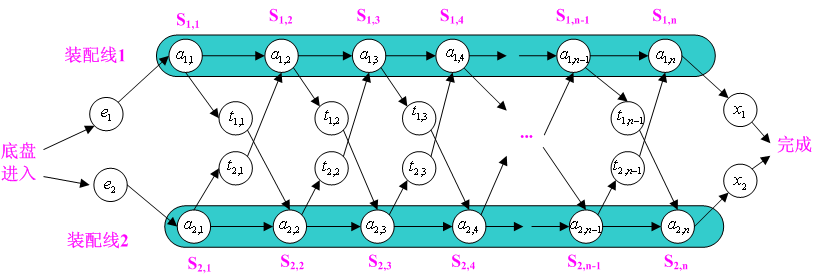

　　装配过程的时间包括：进入装配线时间e、每装配线上各个装配站执行时间a、从一条装配线移到另外一条装配线的时间t、离开最后一个装配站时间x。举个例子来说明，现在有2条装配线，每条装配线上有6个装配站，各个时间如下图所示：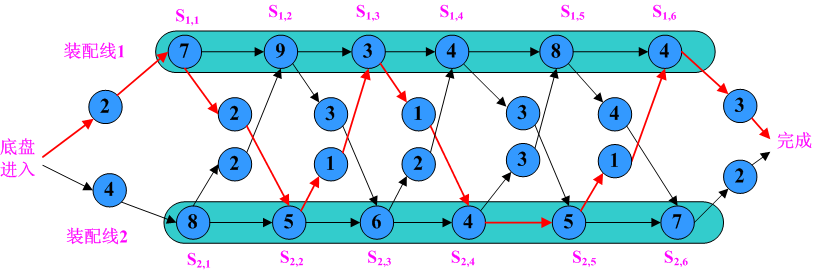

从图中可以看出按照红色箭头方向进行装配汽车最快，时间为38。分别现在装配线1上的装配站1、3和6，装配线2上装配站2、4和5。

3、动态规划解决步骤

（1）描述通过工厂最快线路的结构

　　对于装配线调度问题，一个问题的（找出通过装配站S_i,j的 最快线路）最优解包含了子问题（找出通过S_1,j-1或S_2,j-1的最快线路）的一个最优解，这就是最优子结构。观察一条通过装配站S1,j的最快线路，会发现它必定是经过装配线1或2上装配站j-1。因此通过装配站的最快线路只能以下二者之一：

a)通过装配线S_1,j-1的最快线路，然后直接通过装配站S_i,j；

b)通过装配站S_2,j-1的最快线路，从装配线2移动到装配线1，然后通过装配线S_1,j。

为了解决这个问题，即寻找通过一条装配线上的装配站j的最快线路，需要解决其子问题，即寻找通过两条装配线上的装配站j-1的最快线路。

（2）一个递归的解

　　最终目标是确定底盘通过工厂的所有路线的最快时间，设为f*，令f_i[j]表示一个底盘从起点到装配站S_i,j的最快时间，则f* = min(f₁[n]+x₁,f₂[n]+x₂)。逐步向下推导，直到j=1。

当j=1时: f₁[1] = e₁+a_1,1,f₂[1] = e₂+a_2,1。

当j>1时：f₁[j] = min(f₁[j-1]+a_1,j，f₂[j-1]+t_2,j-1+a_1,j)，f₂[j] = min(f₂[j-1]+a_2,j，f₁[j-1]+t_1,j-1+a_2,j)。

（3）计算最快时间

　　有了递归的解，就可以按照上述的思路编写程序实现，为了避免用递归实现，需要开辟辅助空间来进行，以空间来换取时间，用C语言实现如下所示：

void fastest_way(int a[][N],int t[][N-1],int e[],int x[],int f[][N],int l[][N],int n)
{
    int i,j;
    f[0][0] = e[0] + a[0][0];
    f[1][0] = e[1] + a[1][0];
    l[0][0] = 1;
    l[1][0] = 2;
    for(j=1;j<n;j++)
    {
        if(f[0][j-1] < f[1][j-1] + t[1][j-1])
        {
            f[0][j] = f[0][j-1] + a[0][j];
            l[0][j] = 1;
        }
        else
        {
            f[0][j] = f[1][j-1] + t[1][j-1] + a[0][j];
            l[0][j] = 2;
        }
        if(f[1][j-1] < f[0][j-1] + t[0][j-1])
        {
            f[1][j] = f[1][j-1] + a[1][j];
            l[1][j] = 2;
        }
        else
        {
            f[1][j] = f[0][j-1] + t[0][j-1] + a[1][j];
            l[1][j] = 1;
        }
    }
    if(f[0][n-1] + x[0] < f[1][n-1] + x[1])
    {
        last_f = f[0][n-1] + x[0];
        last_l = 1;
    }
    else
    {
        last_f = f[1][n-1] + x[1];
        last_l = 2;
    }
}

（4）构造通过工厂的最快线路

　　有第三步骤已经计算出来并记录了每个装配站所在的装配线编号，故可以按照以站号递减顺序直接输出，程序如下所示：

void print_station(int l[][N],int last_l,int n)
{
    int i = last_l;
    int j;
    printf("line %d,station %d\n",i,n);
    for(j=n-1;j>0;--j)
    {
        i = l[i-1][j];
        printf("line %d,station %d\n",i,j);
    }
}

　　若是按照站号递增顺序输出，则需通过递归进行实现，程序如下所示：

void print_station_recursive(int l[][N],int last_l,int n)
{
    int i = last_l;
    if(n == 1)
        printf("line %d,station %d\n",i,n);
    else
    {
         print_station_recursive(l,l[i-1][n-1],n-1);
         printf("line %d,station %d\n",i,n);
    }

}

4、编程实现

根据上面的分析，采用C语言实现如下：

#include <stdio.h>
#include <stdlib.h>

#define N 6

void fastest_way(int a[][N],int t[][N-1],int e[],int x[],int f[][N],int l[][N],int n);
void print_station(int l[][N],int last_l,int n);
void print_station_recursive();
//全局变量，last_t表示最短时间,last_l表示最后一个装配站所在的装配线编号
int last_f,last_l;

int main()
{
    int a[2][6] = {{7,9,3,4,8,4},{8,5,6,4,5,7}};
    int t[2][5] = {{2,3,1,3,4},{2,1,2,2,1}};
    int f[2][6] = {0};
    int l[2][6] = {0};
    int e[2] = {2,4};
    int x[2] = {3,2};
    int i,j;
    fastest_way(a,t,e,x,f,l,6);
    //打印输出各个装配线上各个装配站执行的最短时间
    for(i=0;i<2;++i)
    {
        printf("f%d is: ",i+1);
        for(j=0;j<6;++j)
          printf("%d ",f[i][j]);
        printf("\n");
    }
    printf("last_f is: %d\nlast_l is: %d\n",last_f,last_l);
    for(i=0;i<2;++i)
    {
        printf("l%d is: ",i+1);
        for(j=0;j<6;++j)
          printf("%d ",l[i][j]);
        printf("\n");
    }
    print_station(l,last_l,6);
    printf("output sequence by recursive.\n");
    print_station_recursive(l,last_l,6);
    return 0;
}

void fastest_way(int a[][N],int t[][N-1],int e[],int x[],int f[][N],int l[][N],int n)
{
    int i,j;
    f[0][0] = e[0] + a[0][0];
    f[1][0] = e[1] + a[1][0];
    l[0][0] = 1;
    l[1][0] = 2;
    for(j=1;j<n;j++)
    {
        if(f[0][j-1] < f[1][j-1] + t[1][j-1])
        {
            f[0][j] = f[0][j-1] + a[0][j];
            l[0][j] = 1;
        }
        else
        {
            f[0][j] = f[1][j-1] + t[1][j-1] + a[0][j];
            l[0][j] = 2;
        }
        if(f[1][j-1] < f[0][j-1] + t[0][j-1])
        {
            f[1][j] = f[1][j-1] + a[1][j];
            l[1][j] = 2;
        }
        else
        {
            f[1][j] = f[0][j-1] + t[0][j-1] + a[1][j];
            l[1][j] = 1;
        }
    }
    if(f[0][n-1] + x[0] < f[1][n-1] + x[1])
    {
        last_f = f[0][n-1] + x[0];
        last_l = 1;
    }
    else
    {
        last_f = f[1][n-1] + x[1];
        last_l = 2;
    }
}

void print_station(int l[][N],int last_l,int n)
{
    int i = last_l;
    int j;
    printf("line %d,station %d\n",i,n);
    for(j=n-1;j>0;--j)
    {
        i = l[i-1][j];
        printf("line %d,station %d\n",i,j);
    }
}
void print_station_recursive(int l[][N],int last_l,int n)
{
    int i = last_l;
    if(n == 1)
        printf("line %d,station %d\n",i,n);
    else
    {
         print_station_recursive(l,l[i-1][n-1],n-1);
         printf("line %d,station %d\n",i,n);
    }

}

程序执行结果如下所示：

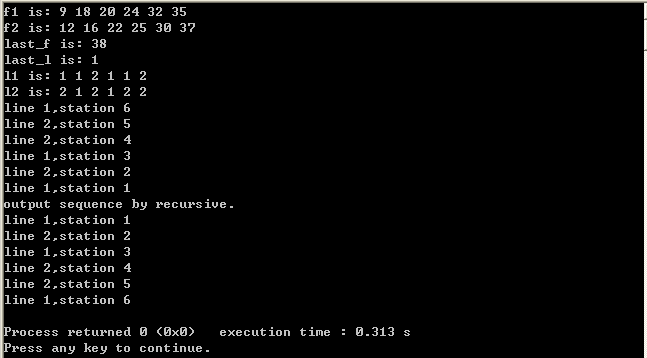
5、总结

　　动态规划是个非常有效的设计方法，要善于用动态规划去分析问题，重点是如何发现子问题的结构。最优子结构在问题域中以两种方式变化（在找出这两个问题的解之后，构造出原问题的最优子结构往往就不是难事了）：

a) 有多少个子问题被用在原问题的一个最优解中
b) 在决定一个最优解中使用哪些子问题有多少个选择