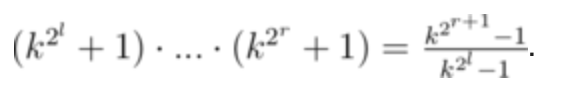学到的东西
- 不知道gcd时不妨先假设为d,然后为了满足全部式子说不定可以得到d的取值范围。
- 幂上带幂考虑欧拉定理的使用。
- 有几个特殊情况会破坏公式的完美不要紧,看看特殊情况是否能简便地判定。
- 连乘公式,证明方法是右边分母乘到左边就都消了:
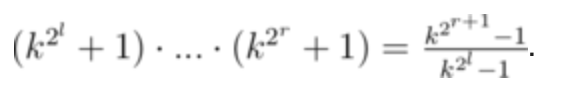
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
int T, k, p;
ll l, r;
ll ksm(int a, ll b, int mod) {
ll res = 1;
for (; b; b >>= 1) {
if (b & 1) res = res * a % mod;
a = (ll)a * a % mod;
}
return res;
}
ll calc(int k, ll l, ll r, int p) {
if (k % p == 0) return 1;//欧拉定理的前提是k、p互质
ll t = ksm(2, l, p - 1);
ll q = (ksm(k, t, p) - 1 + p) % p;
if (!q) return ksm(2, r - l + 1, p);//分母为0
ll y = ksm(2, r + 1, p - 1);
ll res = (ksm(k, y, p) - 1 + p) % p * ksm(q, p - 2, p) % p;
return res;
}
int main() {
ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);
for (cin >> T; T--;) {
cin >> k >> l >> r >> p;
if (p == 2) {
cout << (k % 2 ? 0 : 1) << '
';
} else {
ll MUL = calc(k, l, r, p);
if (k % 2) {
MUL = MUL * ksm(ksm(2, r - l, p), p - 2, p) % p;
}
cout << MUL << '
';
}
}
}