BZOJ3994
大佬们推公式的手段是怎么学到的……qwq完全想不到啊qwq
学习的是这篇博客的推公式。
要点节选:
1.结论:d(i*j)是i*j的约数个数,则

2.又用到莫比乌斯函数的性质
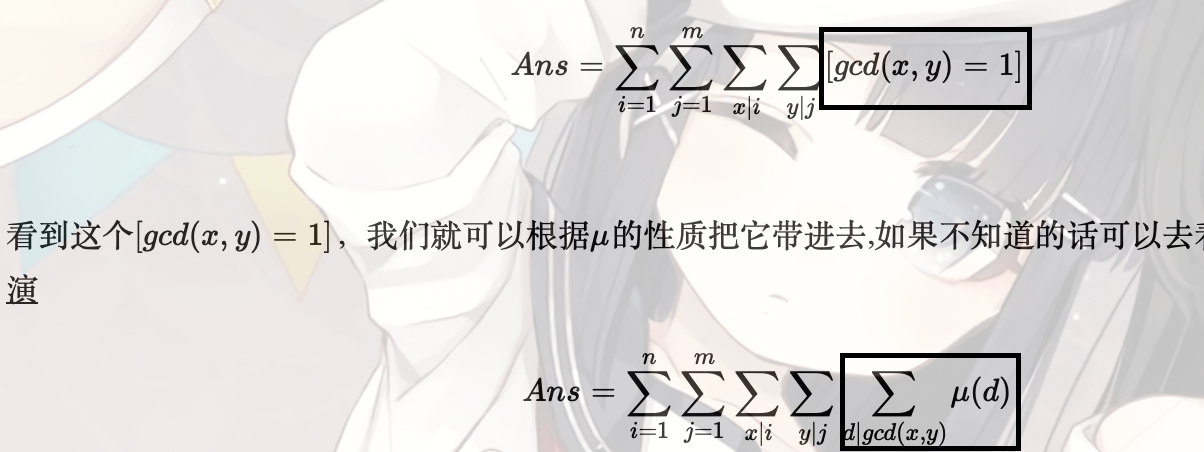
3.枚举项的更换。约数整除枚举的和搭配真值式往往可以替代为常数块,而直接枚举符合真值的数可以省去真值。
数学推导出来以后,代码就不复杂了。

1 #pragma comment(linker, "/STACK:1024000000,1024000000") 2 #include <cstdio> 3 #include <cstring> 4 #include <cstdlib> 5 #include <cmath> 6 #include <ctime> 7 #include <cctype> 8 #include <climits> 9 #include <iostream> 10 #include <iomanip> 11 #include <algorithm> 12 #include <string> 13 #include <sstream> 14 #include <stack> 15 #include <queue> 16 #include <set> 17 #include <map> 18 #include <vector> 19 #include <list> 20 #include <fstream> 21 #include <bitset> 22 #define init(a, b) memset(a, b, sizeof(a)) 23 #define rep(i, a, b) for (int i = a; i <= b; i++) 24 #define irep(i, a, b) for (int i = a; i >= b; i--) 25 using namespace std; 26 27 typedef double db; 28 typedef long long ll; 29 typedef unsigned long long ull; 30 typedef pair<int, int> P; 31 const int inf = 0x3f3f3f3f; 32 const ll INF = 1e18; 33 34 template <typename T> void read(T &x) { 35 x = 0; 36 int s = 1, c = getchar(); 37 for (; !isdigit(c); c = getchar()) 38 if (c == '-') s = -1; 39 for (; isdigit(c); c = getchar()) 40 x = x * 10 + c - 48; 41 x *= s; 42 } 43 44 template <typename T> void write(T x) { 45 if (x < 0) x = -x, putchar('-'); 46 if (x > 9) write(x / 10); 47 putchar(x % 10 + '0'); 48 } 49 50 template <typename T> void writeln(T x) { 51 write(x); 52 puts(""); 53 } 54 55 const int maxn = 5e4 + 5; 56 int T, n, m; 57 int mu[maxn], primes[maxn], tot; 58 ll sum[maxn], g[maxn]; 59 bool vis[maxn]; 60 61 void pre(int n) { 62 mu[1] = 1; 63 rep(i, 2, n) { 64 if (!vis[i]) { 65 mu[i] = -1; 66 primes[++tot] = i; 67 } 68 for (int j = 1; j <= tot && primes[j] * i <= n; j++) { 69 vis[primes[j] * i] = true; 70 if (i % primes[j] == 0) break; 71 mu[primes[j] * i] = -mu[i]; 72 } 73 } 74 rep(i, 1, n) sum[i] = sum[i - 1] + mu[i]; 75 rep(t, 1, n) { 76 ll tmp = 0ll; 77 for (int l = 1, r; l <= t; l = r + 1) { 78 r = t / (t / l); 79 tmp += (ll)(r - l + 1) * (t / l); 80 } 81 g[t] = tmp; 82 } 83 } 84 85 int main() { 86 pre(maxn - 5); 87 for (read(T); T; T--) { 88 read(n), read(m); 89 if (n > m) swap(n, m); 90 ll ans = 0ll; 91 for (int l = 1, r; l <= n; l = r + 1) { 92 r = min(n / (n / l), m / (m / l)); 93 ans += (sum[r] - sum[l - 1]) * g[n / l] * g[m / l]; 94 } 95 writeln(ans); 96 } 97 return 0; 98 }
BZOJ3529
首先是得推公式, 学习的这个PPT,核心:


这公式根本想不到啊嘤~
那么这样子以后就是操作问题了:1.离线,按a的大小把询问排序;2.不断往树状数组里插入符合当前a值的F*mu;3.对于每个询问a,分块得到ans,这时往常的sum[r]-sum[l-1]就用BIT的query(r) - query(l-1)来得到了,特殊的前缀和。3.取模的方法也很有趣,自由爆int……

1 #pragma comment(linker, "/STACK:1024000000,1024000000") 2 #include <cstdio> 3 #include <cstring> 4 #include <cstdlib> 5 #include <cmath> 6 #include <ctime> 7 #include <cctype> 8 #include <climits> 9 #include <iostream> 10 #include <iomanip> 11 #include <algorithm> 12 #include <string> 13 #include <sstream> 14 #include <stack> 15 #include <queue> 16 #include <set> 17 #include <map> 18 #include <vector> 19 #include <list> 20 #include <fstream> 21 #include <bitset> 22 #define init(a, b) memset(a, b, sizeof(a)) 23 #define rep(i, a, b) for (int i = a; i <= b; i++) 24 #define irep(i, a, b) for (int i = a; i >= b; i--) 25 using namespace std; 26 27 typedef double db; 28 typedef long long ll; 29 typedef unsigned long long ull; 30 typedef pair<int, int> P; 31 const int inf = 0x3f3f3f3f; 32 const ll INF = 1e18; 33 34 template <typename T> void read(T &x) { 35 x = 0; 36 int s = 1, c = getchar(); 37 for (; !isdigit(c); c = getchar()) 38 if (c == '-') s = -1; 39 for (; isdigit(c); c = getchar()) 40 x = x * 10 + c - 48; 41 x *= s; 42 } 43 44 template <typename T> void write(T x) { 45 if (x < 0) x = -x, putchar('-'); 46 if (x > 9) write(x / 10); 47 putchar(x % 10 + '0'); 48 } 49 50 template <typename T> void writeln(T x) { 51 write(x); 52 puts(""); 53 } 54 55 const int maxn = 1e5 + 5, maxq = 2e4 + 5; 56 int n, m, a, Q, mx; 57 int mu[maxn], primes[maxn], tot, ans[maxq]; 58 bool vis[maxn]; 59 P F[maxn]; 60 61 struct node { 62 int n, m, a, id; 63 64 bool operator < (const node &b) const { 65 return a < b.a; 66 } 67 }T[maxq]; 68 69 struct BIT { 70 int t[maxn]; 71 72 void add(int x, int val) { 73 for (int i = x; i <= mx; i += i&-i) 74 t[i] += val; 75 } 76 77 int query(int x) { 78 int ret = 0; 79 for (int i = x; i; i -= i&-i) 80 ret += t[i]; 81 return ret; 82 } 83 }bit; 84 85 void pre(int n) { 86 mu[1] = 1; 87 rep(i, 2, n) { 88 if (!vis[i]) { 89 mu[i] = -1; 90 primes[++tot] = i; 91 } 92 for (int j = 1; j <= tot && primes[j] * i <= n; j++) { 93 vis[primes[j] * i] = true; 94 if (i % primes[j] == 0) break; 95 mu[primes[j] * i] = -mu[i]; 96 } 97 } 98 rep(i, 1, n) { 99 for (int j = i; j <= n; j += i) { 100 F[j].first += i; 101 } 102 } 103 rep(i, 1, n) F[i].second = i; 104 } 105 106 void solve(int i) { 107 int id = T[i].id, n = T[i].n, m = T[i].m; 108 for (int l = 1, r; l <= n; l = r + 1) { 109 r = min(n / (n / l), m / (m / l)); 110 ans[id] += (n / l) * (m / l) * (bit.query(r) - bit.query(l - 1)); 111 } 112 } 113 114 int main() { 115 read(Q); 116 rep(i, 1, Q) { 117 read(n), read(m), read(a); 118 if (n > m) swap(n, m); 119 T[i] = {n, m, a, i}; 120 mx = max(mx, n); 121 } 122 pre(mx); 123 sort(F + 1, F + 1 + mx); 124 sort(T + 1, T + 1 + Q); 125 int now = 0; 126 rep(i, 1, Q) { 127 while(now + 1 <= mx && F[now + 1].first <= T[i].a) { 128 now++; 129 for (int j = F[now].second; j <= mx; j += F[now].second) 130 bit.add(j, F[now].first * mu[j / F[now].second]); 131 } 132 solve(i); 133 } 134 rep(i, 1, Q) writeln(ans[i]&0x7fffffff); 135 return 0; 136 }
-----未完待续-----
