序言
1、符号主义、贝叶斯派、联结主义、进化主义、行为类比主义(机器学习的五大流派):
参考:本书1.5节及https://blog.csdn.net/rogerchen1983/article/details/79681463;
第一章 绪论
1、1997年,Tom Mitchell对机器学习的定义引入了三个概念:经验Experience(E)、任务Task(T)、任务完成效果的衡量指标Performance measure(P)。将机器学习定义为:假设用P来评估计算机程序在某任务类T上的性能,若一个程序通过利用经验E在T中任务上获得了性能改善,则我们说关于T和P,该程序对E进行了学习。即在有了经验E的帮助后,机器完成任务T的衡量指标P变得更好了。
2、奥卡姆剃刀原理:“如无必要,勿增实体”,即“简单有效原理”。周志华西瓜书中描述为:“若有多个假设与观察一致,则选择最简单的那个”。
3、没有免费的午餐定理:没有免费午餐定理(No Free Lunch,简称NFL),该定理的结论是,由于对所有可能函数的相互补偿,最优化算法的性能是等价的。即脱离具体的问题,空泛地谈论“什么学习算法最好”毫无意义。
第二章 模型评估与选择
1、P问题、NP问题、NPC问题 NP hard问题
在计算机领域,一般可以将问题分为可解问题和不可解问题。不可解问题也可以分为两类:一类如停机问题,的确无解;另一类虽然有解,但时间复杂度很高。可解问题也分为多项式问题(Polynomial Problem,P问题)和非确定性多项式问题(NondeterministicPolynomial Problem,NP问题)。
2.、评估模型泛化误差的方法
2.1、留出法
2.2、交叉验证法(k次交叉验证、p次k折交叉验证、留一法)
适用于数据量足够的情况;
任何评估方法不一定比其他评估方法更准确,“没有免费的午餐”定理对实验评估方法同样适用。
2.3、自助法
适用于数据集较小、难以进行有效划分训练/测试集的情况。能从初始数据中产生多个不同的训练集,对集成学习有较大好处。但自助法产生的数据集改变了初始数据的分布,会引入估计偏差。
3.、评估不同模型泛化性能(分隔出验证集进行调参,并在测试集上进行测试)
将样本数据集分为测试集和训练数据,训练数据进一步分为训练集和验证集。使用验证集进行模型的选择和调参,使用测试集来估计模型在实际使用时的泛化能力。
训练集、验证集、测试集:
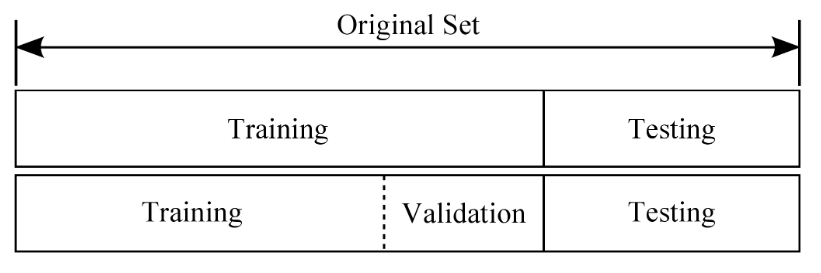
4、性能度量(评估模型的泛化性能)
4.1、回归任务:将模型预测结果与真实值进行比较,计算“误差”,如:
①:欧式、曼哈顿、切比雪夫距离、闵可夫斯基距离,如:回归任务中常用均方误差;
②:余弦距离;
③:汉明距离;
④:马哈拉诺斯比斯距离;
⑤:相关系数;
4.2、分类任务: ①:错误率、精度;
②:二分类任务:混淆矩阵、查准率、查全率、P-R曲线(查准率-查全率曲线)图、面积度量标准(度量学习器的查准率、查全率性能)、平衡点(BEP)性能度量标准、F1度量标准、Fβ度量标准;
③:多分类任务:两两类别之间组建n个混淆矩阵、宏查准率、宏查全率、宏F1、微查准率、微查全率、微F1;
④:ROC曲线(真正例TPR率-假正例FPR率曲线)、AUC面积度量法;
⑤:代价敏感错误率、代价曲线;
5、比较检验(以错误率为例,分析学习器的泛化性能是否良好?有多大的把握(显著度)?)
5.1、概率论知识补充
常用离散型分布:单点分布(退化分布)、(0-1)分布(两点分布或伯努利分布)、二项分布、负二项分布(帕斯卡分布)、几何分布、超几何分布、泊松分布;
常用连续型分布: 均匀分布、正态分布(高斯分布)、对数正态分布、逆高斯分布、Γ分布( 伽玛分布 ) 、指数分布(负指数分布)、卡方分布、非中心卡方分布、韦布尔分布、
拉普拉斯分布、瑞利分布、帕雷托分布、极值分布、逻辑斯蒂分布、β分布 、柯西分布、t 分布(学生氏分布)、非中心 t 分布、F分布、非中心 F分布;
5.2、常用的分布
参考:https://zhuanlan.zhihu.com/p/47609519

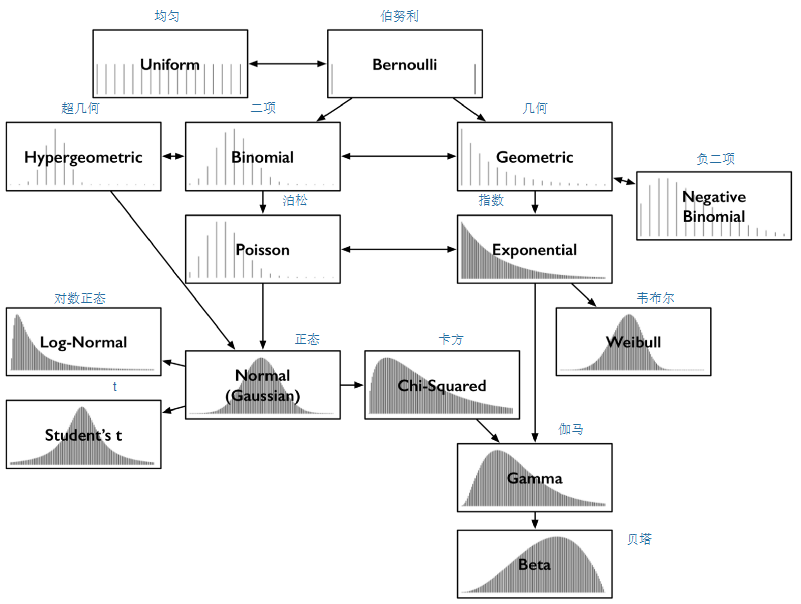
5.3、常用的分布所解决的问题
大数定理:在随机事件的大量重复出现中,往往呈现几乎必然的规律,这个规律就是大数定律。
0-1分布(两点分布或伯努利分布)、均匀分布:一次随机事件发生某一结果的概率;
二项分布、超几何分布:n次伯努利试验(或有放回抽样试验)中事件A恰好发生k次的概率。超几何分布为不放回抽样时的概率;
几何分布、负二项分布:前k-1次皆失败,第k次成功的概率。负二项分布为r次失败(成功)前成功(失败)的次数;
泊松分布:特定时间里发生n个事件的机率。当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。通常当n≧20,p≦0.05时,就可以用泊松分布近似计算。事实上,泊松分布正是由二项分布推导而来的;
指数分布:要等到一个随机事件发生,需要经历多久时间。给定一个某段时间内发生次数遵循泊松分布的事件,那么事件间隔时间遵循参数λ相同的指数分布。
正态分布:
中心极限定理:①:独立同分布的中心极限定理:在实际工作中,只要n足够大,便可以把独立同分布的随机变量之和当作正态变量;
②:棣莫佛-拉普拉斯定理:正态分布是二项分布的极限分布;
③:不同分布的中心极限定理:随机变量如果是有大量独立的而且均匀的随机变量相加而成,那么它的分布将近似于正态分布。
t分布、卡方分布:t分布用于推断正态分布的均值。检验基于观测值和理论值的差(假定差遵循正态分布)的平方和;
伽玛分布和贝塔分布:伽玛分布可以用来建模接下来第n个事件发生前的时间。Beta分布是一个定义在[0,1]区间上的连续概率分布族,它有两个正值参数,称为形状参数,一般用αα和ββ表示。在贝叶斯推断中,Beta分布是Bernoulli、二项分布、负二项分布和几何分布的共轭先验分布;
5.4、常用区间估计与假设检验公式表
参考:https://wenku.baidu.com/view/1ae0a2b8a56e58fafab069dc5022aaea998f41ef.html


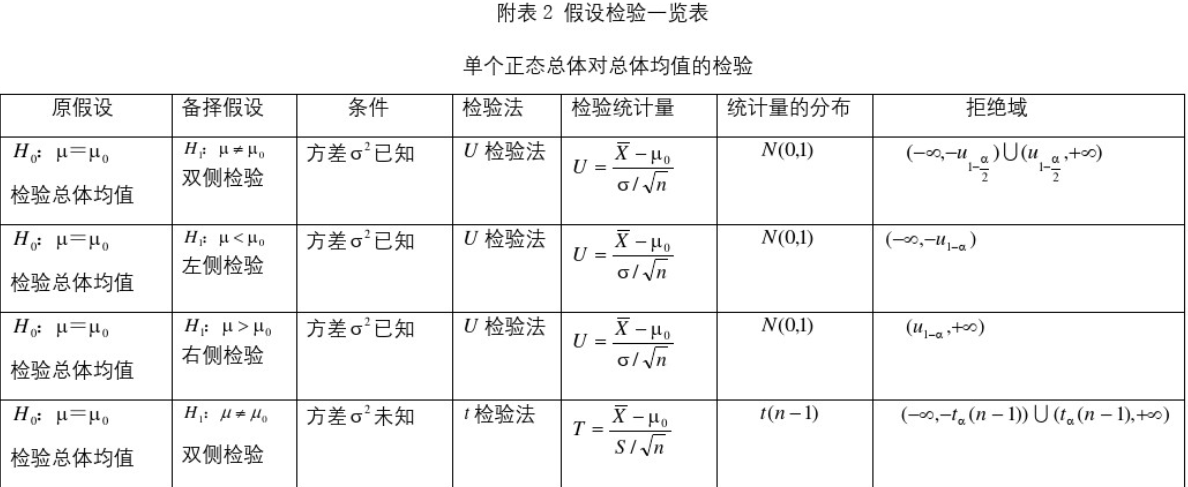

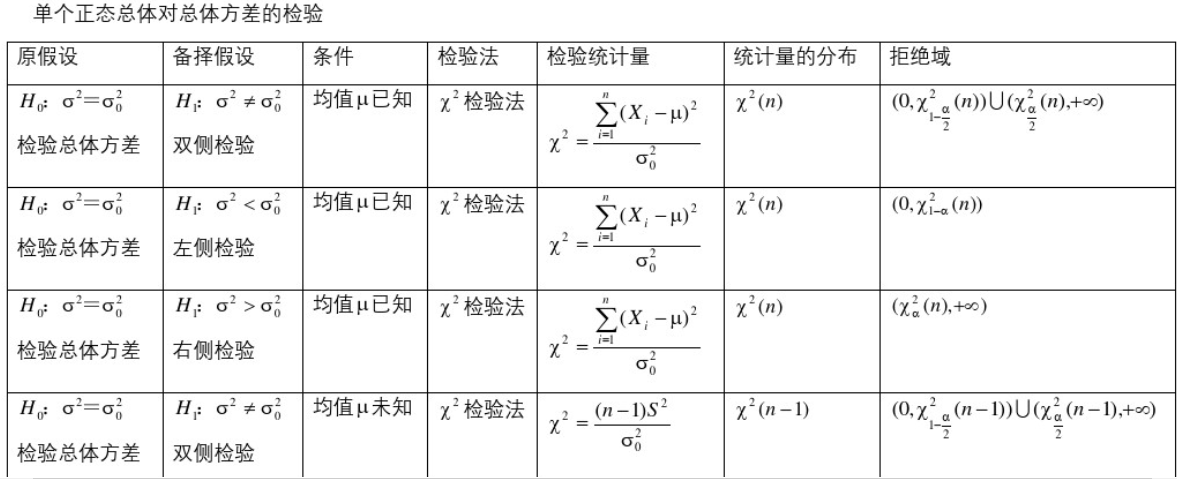

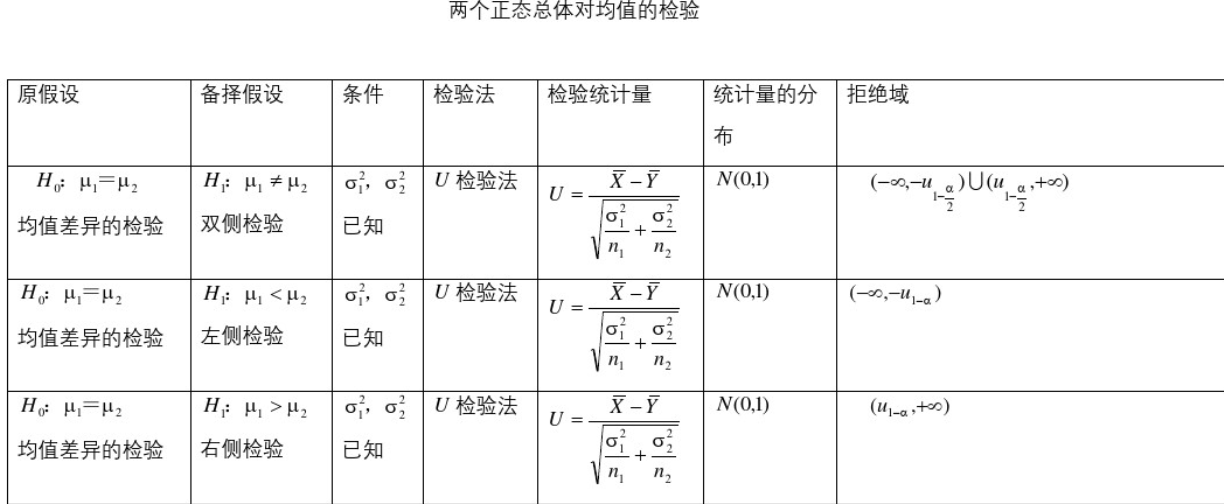


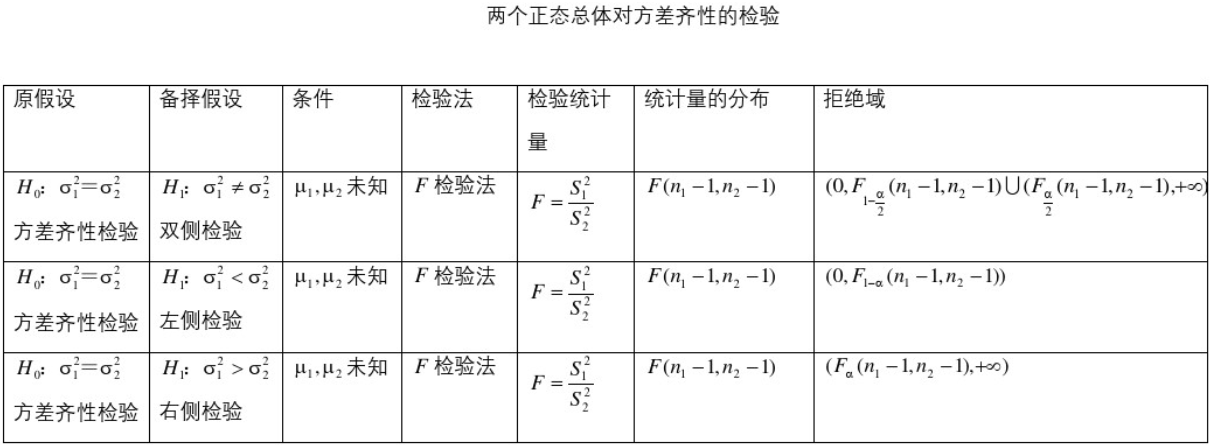
5.5、常用假设检验
参考:https://www.cnblogs.com/hust-chen/p/8643973.html
5.6、不同学习器,相同测试集,交叉验证t检验
5.7、不同学习器,相同测试集,McNemar
5.8、不同学习器,不同测试集,Friedman检验与Nemenyi后验
6、偏差与方差
偏差刻画了学习算法本身的拟合能力;(欠拟合);
方差刻画了数据扰动所造成的影响;(过拟合);
噪声刻画了学习问题本身的难易程度;
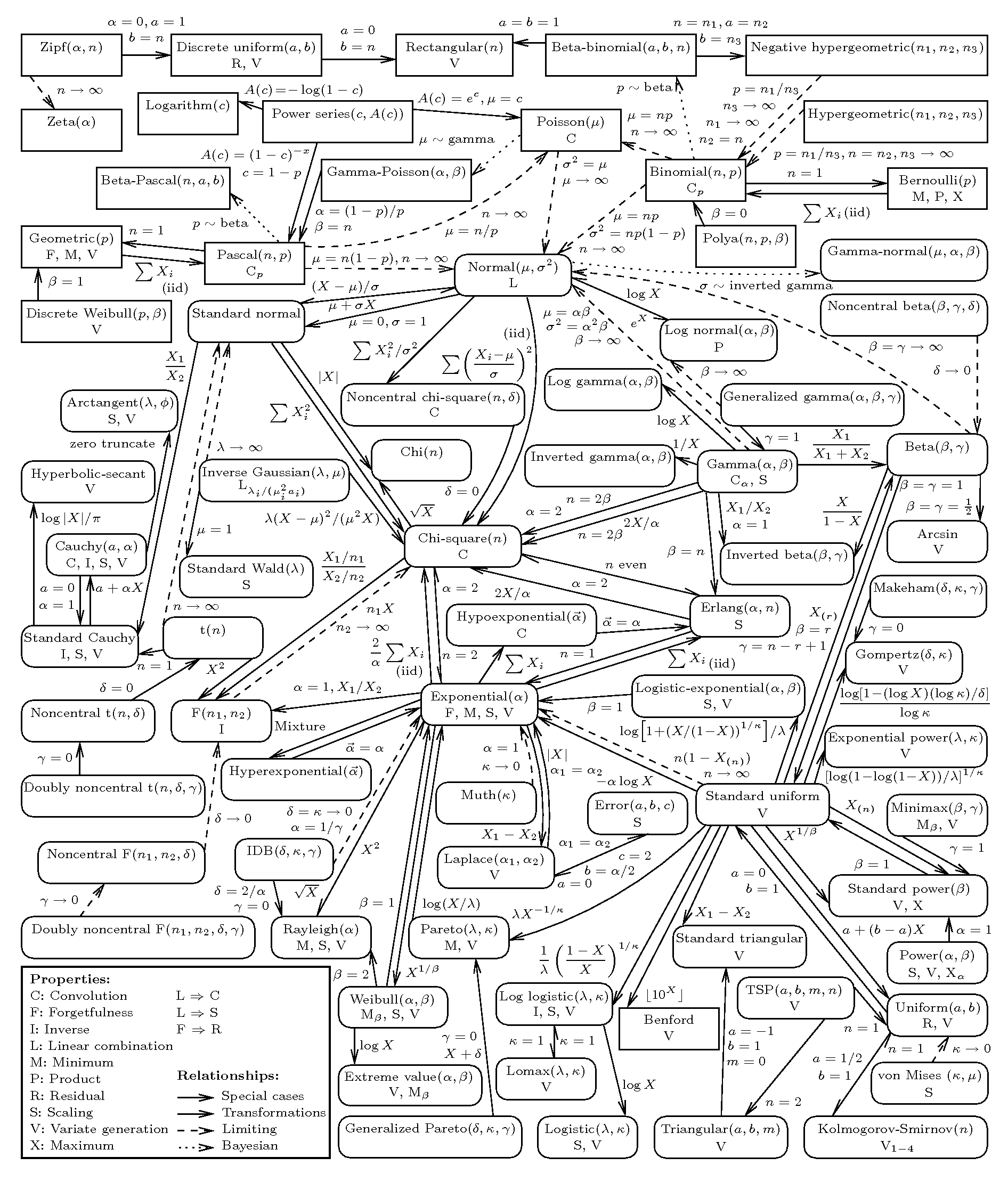
附录 常用概率分布间的关系
参考:http://www.math.wm.edu/~leemis/chart/UDR/UDR.html
http://www.math.wm.edu/~leemis/2008amstat.pdf